Dungeons & Qubits: Ramsey and Frequency Tracking

In the last blog post, we discussed how the Hadamard Pulse Processing Unit (PPU) enables real-time craziness and provides the four stable pillars of quantum control (parametric waveform generation & manipulation and processing & control flow) in qubit timescales.
Today, I would like to show you just how powerful real-time control and feedback really are. We will dive into the lab dungeon to fight two everyday problems that nest there. In order of difficulty, measuring the qubit dephasing time and estimating resonance frequency drifts. Together you and I are going to combat them using the Quantum Orchestration Platform, its OPX, and the PPU at its core by tapping into Ramsey measurement and qubit-frequency tracking protocols.
Ready? Grab your axe and brace yourself.
 Level 1: Ramsey Measurement
Level 1: Ramsey Measurement 
Here we face the challenge of quantifying the qubit dephasing time T2* to get an idea of how long we have to run operations before quantum information is lost. To measure this quantity, labs everywhere use Ramsey sequences (see Fig.1). The protocol consists of playing a 𝝅/2 pulse, followed by a waiting time, or interpulse delay 𝛕, and then another 𝝅/2 pulse. Then, we measure the qubit to monitor its state. The rotations on the Bloch sphere are arranged in a way that changes the qubit state from |0> to |1> and back. This way, we can measure the timescale of the dephasing, which makes the system deviate from this pattern.
Our OBJECTIVES are to optimize this widely-used procedure to move on to more fun stuff:

MAKE IT SIMPLE
We need to make it easier to implement and use a Ramsey protocol inside other sequences. Basic protocols must become no-brainers to get to crazier stuff.

SPEED IT UP
The protocol must run faster. We don’t want to wait hours for a graph, and we have a limited time to perform sequences, so every nanosecond matters.

MAKE IT FLEXIBLE & REAL-TIME
The next dungeons in our quantum future require flexibility and real-time feedback. We must be able to measure and redefine the next pulse in much less than the T2*.
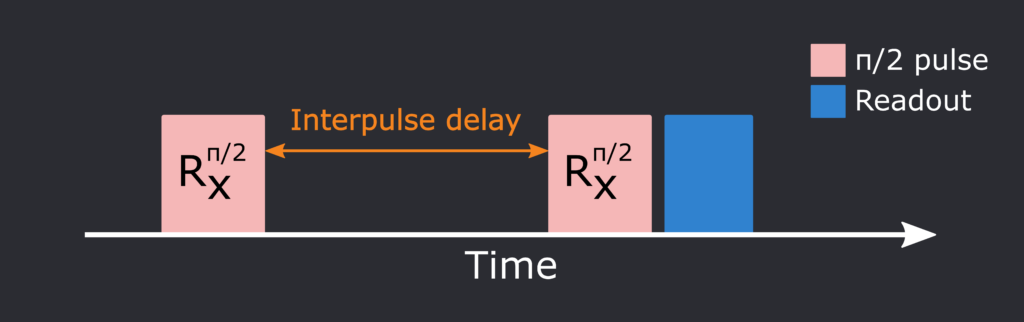
Ramsey Sequence in QUA
Let’s get to the action. In QUA, our programming language dedicated to quantum control, a Ramsey sequence (as any other) can be comfortably placed in a macro, e.g. within Python:
def ramsey(tau, qubit, resonator, state): # sometimes we need a resonator, sometimes not
wait(100, qubit) # PPU waits, no need to send zeros to memory
play("pi_half", qubit) # Apply precalibrated pi/2 pulses with delay tau
wait(tau, qubit)
play("pi_half", qubit)
align(qubit, resonator) # SSRO must happen after qubit oper.
state = SSRO(resonator, state) # Measure the qubit, return 1 or 0.
play("pi", qubit, condition=(state==1)) # Perform active reset -
# only play pulse if qubit is in excited state
return stateWe do it with little more than pseudocode: just play a pulse, wait, play a pulse, measure (check out our SSRO macro!). The 𝝅/2 pulses are just a few-data-points waveforms drawn from a configuration file with pre-calibrated parameters.
With pulse-level logical commands such as wait(), we avoid the whole “send many zeros to the AWG” thing. As a matter of fact, you won’t need an AWG at all, so there’s that. To loading and compilation times, we say: no more! The PPU understands the language we use to sketch ideas on the whiteboard. If we go further down this route, we won’t even find idle time to grab a coffee. Times really are a-changing, aren’t they?
In our basic Ramsey block, we use a wait() command to ensure the qubit is in its ground state. Of course, if we have a way to reset it actively, this becomes unnecessary. The way you explain active reset to a fellow physicist is a play() command sending a ”pi” pulse to our qubit, conditionally on its state. A one-liner in QUA, which runs in less than 200ns.
The align() command tells the PPU to time-synchronize elements, so one will wait for the other. If you’ve ever dealt with programming repeat-until-success protocols and time-synchronized stuff on FPGAs, you know this is a game-changer: the difference between months of development vs. hours or minutes. Unless specified via an align(), every command on different qubits runs concurrently and independently on distinct PPU threads. Two separate setups can run two different experiments simultaneously, with one box.
We repeat the Ramsey macro for different values of the interpulse delay 𝛕 for a 1-dimensional Ramsey and detuning for a 2-dimensional Ramsey (see the result in Fig.2). Let’s also wrap this in a macro; after all, why not?
def two_d_ramsey(qubit, resonator, frq_range, frq_step, tau_range, tau_step, map):
with for_(f, frq_range[1], f < frq_range[2], f + frq_step): # Loop over detuning
update_frequency(qubit, f) # Update freq. dynamically
with for_(t, tau_range[1], t < tau_range[2], t + tau_step): # Loop over delay
map[f, t] = ramsey(t, qubit, resonator, state) # Update pixel on mapLoops and other control flow statements are also understood by the PPU and run in real-time on the FPGA (real-time logic rather than compiled unwrapped code). Real-time variables are updated and used for calculations or dynamically compared to thresholds while you write everything just as you would expect. update_frequency() updates the frequency applied to the qubit, duh.
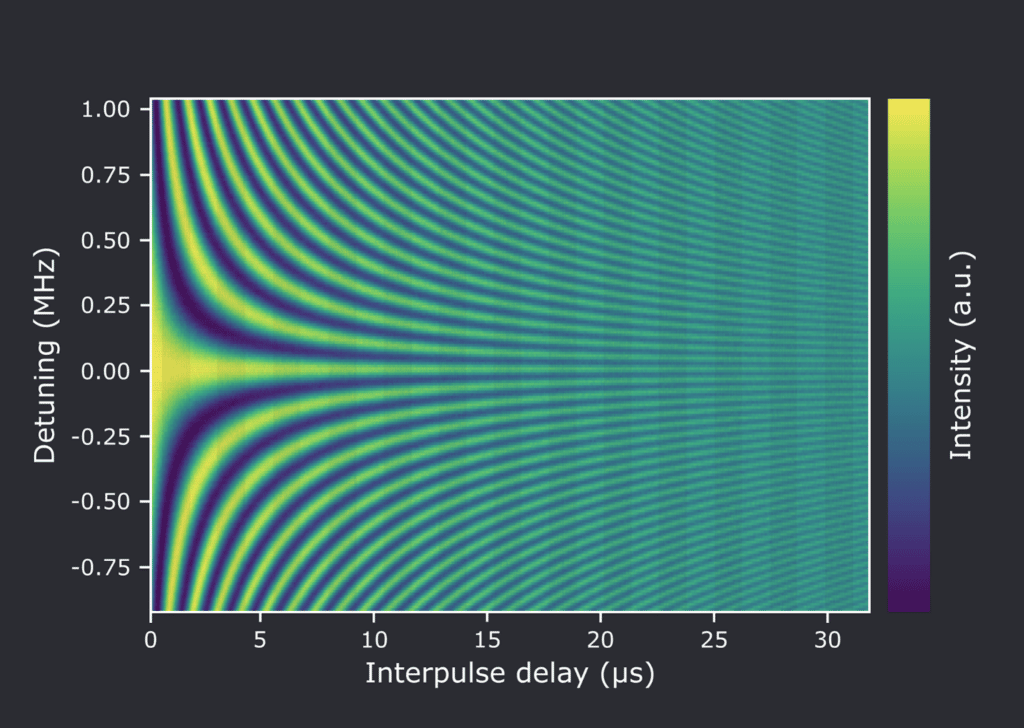
So we implemented 1D and 2D Ramsey macros with just a few lines of code: Simple.
Real-time logic simplifies the system and runs with the lowest possible latencies: Faster.
Every variable can be a real-time variable living on FPGA: Flexible and Real-Time.

Well done! Now let’s go one level deeper into the dungeon.
 Level 2: Frequency Tracking
Level 2: Frequency Tracking 
The next boss we’ll be facing in our campaign is the drifts in resonance frequency every qubit experiences. To drive and use our QPU correctly we need to make sure we hit the spot. We need to hit a moving target. The challenges are clear, and our previous OBJECTIVES have slightly changed:

MAKE IT SIMPLE enough to AUTOMATE IT
Basic protocols must become no-brainers. We know this, of course. But they need to be simple enough to be automated to become part of the automated routine.

SPEED IT UP to be more FREQUENT
Of course, we do not want to wait hours for a graph, but to get to the really crazy sequences, we need to perform the easy ones all the time.

MAKE IT FLEXIBLE & REAL-TIME to run during other experiments
Dephasing times are on us, so our basic calibration routines must be able to run while we perform other longer experiments.
Active Frequency Tracking Sequence in QUA
The qubit frequency often drifts during long sequences with many repetitions due to minor imperfections and perturbations, thus reducing our ability to probe the qubits correctly. It is essential that for every blow, we calibrate our aim, yet this proved challenging with a party of general-purpose equipment, as it requires calculations and corrections in real-time using values calculated during the experiment. To get even close, adventurers must program FPGA and ADwin controllers to captain the fellowship of instruments, resulting in painfully long setup times and limitations due to inter-boxes latencies.
The Quantum Orchestration Platform resolves all that mess with one unified solution dedicated to real-time control. The Hadamard PPU at the core of the OPX works in “qubit-times” by default and is programmed easily in QUA, our high-level language that gets compiled automatically to FPGA assembly.
Our fancy experiment can now be written as a simple QUA code because we’ve handled the Ramsey challenge. I want to use randomized benchmarking as an example of a “fancy experiment” because we’d get to roll dice, and who doesn’t love rolling dice? Here goes:
with program() as your_experiment: # e.g. randomized_benchmarking
n = declare(int) # define real-time var. living on FPGA
freq = declare(int)
res = declare(bool)
qubit_if = declare(int, value=original_if)
with for_(n, 0, n < 1e6, n + 1): # run as many iterations as you need
randomized_benchmarking(qubit) # macro including any of your experiments
active_freq_tracking(qubit, qubit_if) # experiment runs with active trackingHere the active frequency tracking is wrapped into a macro. We get to run it within each iteration of any experiment, ensuring that drifts remain virtually zero at all times. Let’s see how the inner workings of the tracking macro look:
def active_freq_tracking(qubit, resonator, qubit_if, df, threshold):
n = declare(int)
state_minus = declare(bool)
state_plus = declare(bool)
diff = declare(int)
phi = declare(int)
delta_f = declare(int)
assign(phi, 0)
with for_(n, 0, n < 2000, n + 1): # Loop any number of times
update_frequency(qubit, qubit_if - df) # Ramsey with lower frequency
state_minus = ramsey(tau, state_minust, resonator, state)
update_frequency(qubit, qubit_if + df) # Ramsey with higher frequency
state_plus = ramsey(tau, state_plus)
assign(diff, state_plus - state_minus) # Difference between st. popul.
assign(phi, phi + diff)
# Freq shift is calculated from phi (via factor)
assign(delta_f, Cast.mul_int_by_fixed(phi, phi_to_freq_factor))
with if_(Math.abs(delta_f) > threshold): # If shift higher than threshold, update
assign(qubit_if, qubit_if + delta_f)
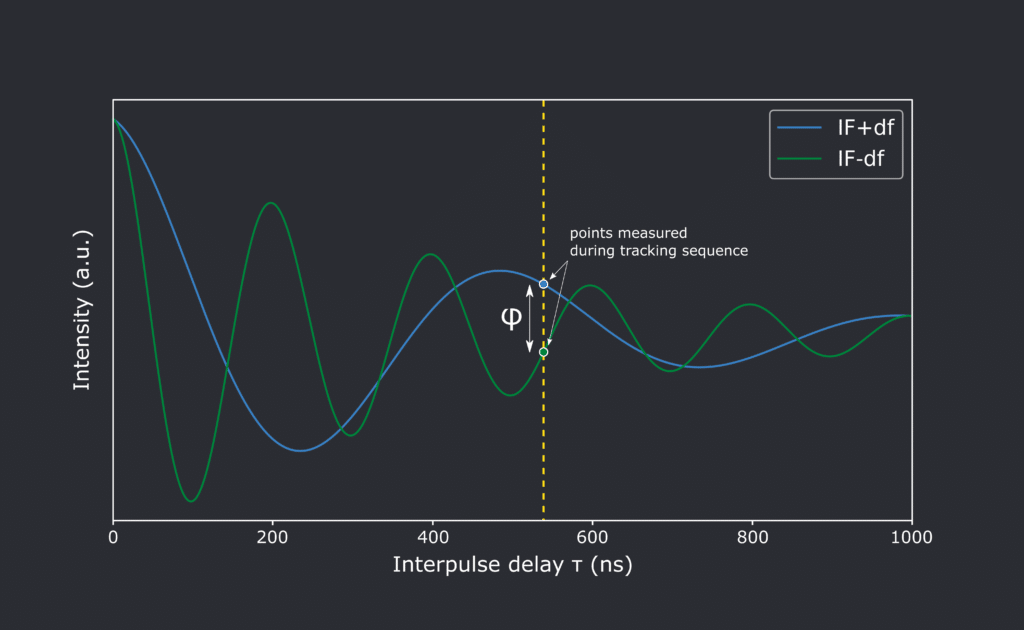
update_frequency(qubit, qubit_if)To actively track the qubit resonant frequency, we use a neat trick: we perform a Ramsey experiment twice with fixed delay but at two different frequencies, the latest estimate of the resonant frequency qubit_if, plus or minus a delta df. This is equivalent to measuring only two pixels in Fig.2, with the same x-axis coordinate, but each with a vertical distance df from the latest value used for the qubit frequency. Since the 2D Ramsey (Fig. 2) is symmetrical on the zero detuning line, a qubit_if exactly matching the resonant frequency would mean zero population difference phi measured. Additionally, \(\phi\) will be proportional to any discrepancy between our applied frequency and the actual qubit frequency. Fig. 3 shows an example of full-Ramsey sweeps to show where the two measured points land.
So here it is! Like a wizard’s trick, we obtain a value for the drift quickly and readily update our drive frequency. We can do this thanks to the real-time capabilities of our PPU, which can update the frequency, make calculations, compare to thresholds, and much more, all in real time, with no communication to the lab computer. To top it off, all of this is packaged into a simple, general, and reusable macro so that tracking the frequency will be just a single additional line of code away when you are ready for your next big experiment. And this is just the tip of the iceberg. Or, should I say, the first-tier dungeon?
 Level 3: Challenge us!
Level 3: Challenge us! 
The next level is for you to define.
I want you to sketch the coolest and most difficult experiment idea you can think of and send it back to me.
Let’s see how challenging it really is.
Until then,
Lorenzo, Wizard Lvl 9
 Level 1: Ramsey Measurement
Level 1: Ramsey Measurement