Quantum Control for Superconducting Qubits
Orchestrating experiments for top performance with ease and at any scale, with a quantum control system ready for the fault tolerance era.
Quantum Machines’ control suite is ideal for superconducting qubit chips. As an example, in Fig. 1 we show how things can be connected in a 4-transmon setup and when scaling to 25 qubits.
Fig. 1 (a) Two OPX+ units are set up to control the MW (2-18 GHz with Octave) and flux tuning (DC-400 MHz baseband) of four transmon qubits, sharing a combined readout. A QDAC-II can be integrated into the flux or drive control to provide ultra-stable low-frequency signals. (b) A single OPX1000 control platform hosting four low-frequency and four microwave modules is used to control 25 transmon qubits with 5 total readouts.
The OPX+ provides radio-frequency (RF, baseband) and microwave (MW, with Octave upconversion) for all control needs up to 18 GHz. Thanks to its unique Pulse Processing Unit (PPU), OPX offers unparalleled capabilities designed for advanced quantum control. The OPX1000 extends these capabilities to encompass 1,000 qubits and beyond. OPX1000 uses one PPU per every low-frequency and microwave module (up to 8 modules of any kind in an OPX1000 chassis). When multiple modules in one or more OPX1000 units are connected they are programmed together and function as a single large controller. Synchronization is assured by the system, and no manual alignment is required. Additionally, with QDAC-II providing DC and low-frequency control with ultra-low noise, QCage24/64 minimizing electromagnetic interference, and QFilter cleaning up our control signals, setting up a state-of-the-art superconducting qubit lab has never been so simple.
In the following sections, we will delve into the unique possibilities enabled by OPX family of PPU processor-based quantum controllers(TM), and explore Quantum Machines’ solutions for superconducting qubits with coding examples ranging from basic to advanced.
Some of the first characterization experiments performed on a system such as the one in Fig. 1 fall under the spectroscopy umbrella. Qubit spectroscopy allows the discovery of the operational frequency of the qubit. For qubit spectroscopy we must repeatedly drive and measure each qubit, while sweeping frequency and averaging the results. We control the OPX operation by writing instructions in QUA, an open-source pulse-level language. The QUA code gets compiled in less than 1 second, and then the sequence runs solely on the PPU, rendering loops and sequences much faster, with no compilation time or memory loading overhead, even for arbitrarily long sequences. For a single qubit, here is how we can code such an experiment in QUA.
# Qubit Spectroscopy QUA code example
with for_(n, 0, n < n_avg, n + 1): #Averaging loop
with for_(*from_array(f, fs)): #Frequency loop
update_frequency("qubit", f)
play("saturation", "qubit")
align("qubit", "resonator")
measure("readout", "resonator", None, demod.full("cos", I), demod.full("sin", Q),)
wait(thermalization_time, "qubit")
# OR play("x180", "qubit", condition = I>threshold) # Active reset
save(I, I_st)
save(Q, Q_st)
save(n, n_st)
# Streaming data to process/fetch during execution
with stream_processing():
I_st.buffer(len(fs)).average().save("I")
Q_st.buffer(len(fs)).average().save("Q")
n_st.save("iteration")
This can be extended into simultaneous multi-qubit operation just by adding one line of code with an additional for loop. This will be similar to other spectroscopy protocols, such as resonator spectroscopy.
We operate in two for loops, for averaging and sweeping, both implemented directly in FPGA (like most QUA functions) and thus running extremely fast. The code for each run is as easy as pseudocode: update frequency, play a saturation pulse, measure, and then reset. Note that OPX, with its parametric pulse generation and on-the-fly manipulation, enhances result quality with averaging performed in the external loop.
The play() command asks the PPU to generate a pulse in real-time, taking a few points from memory and interpolating all others, then changing amplitude and stretching duration as required.
update_frequency(), another native QUA function, allows to change the frequency of all the pulses that would come out of a given channel, and it takes less than 200 ns to perform.
align() requires the PPU to wait that all elements called to be done before continuing, effectively aligning them temporally. This is very useful in most protocols, and a critical element for repeat-until-success sequences (examples below).
The measure() command, measures with demodulation, integration or even time-tagging, depending on needs.
wait() does exactly that, producing a gap in the pulse sequence of a specified amount. In this case it is used to reset the qubit waiting for thermalization_time, but we will later see how to implement active reset for better performance.
We plot an example results of spectroscopy measurements in Fig. 2. We included a resonator spectroscopy for completeness, for which the QUA code does not stray much from the one above.
Fig. 2 – Results of frequency sweeps in resonator (a) and qubit (b) spectroscopy protocols for a superconducting qubit.
Lastly, the stream_processing allows to save, fetch and process data on an ARM processor working in parallel to the PPU, to perform heavier processing, fitting and much more, inside the OPX box and avoid clogging the lab network with unprocessed data. We will skip the stream processing in the codes below, but it is always available for any kind of processing.
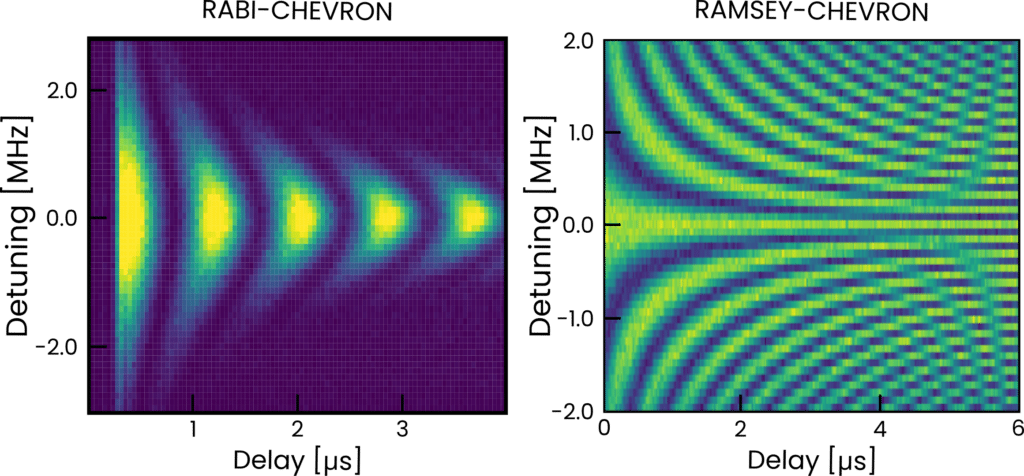
Following spectroscopy, there is many other characterization protocols that can help further our understanding on the qubit, to gather information about coherence times and more. As an example, we take a Ramsey-Chevron map: a loop over many Ramsey runs, changing frequency and interpulse delay. As shown in Fig. 3, a Ramsey sequence is composed of two π/2 pulses with a varying delay between them. Averaging this over many shots we obtain an oscillating probability of finding the qubit in either state, from which the T2* of the qubit can be extracted.

Let’s now see how such a Ramsey-Chevron experiment can be coded in QUA:
# Ramsey-Chevron QUA code example
with for_(n, 0, n < n_avg, n + 1): #Averaging loop
with for_(*from_array(tau, taus)): #Delay loop
with for_(*from_array(f, fs)): #Frequency loop
update_frequency("qubit", f)
play("x90", "qubit")
wait(tau, "qubit")
play("x90", "qubit")
align("qubit", "resonator")
measure(..., I, Q),
active_reset("qubit")
We now notice how simple it is to drive a π- or π/2-pulse once they are calibrated (done with Rabi sequences, not shown here). Most other characterization sequences are written similarly in QUA, with a series of play(), wait() and measure() commands explained above. In this case we introduce the macro active_reset(), that will be defined later, to actively reset a qubit. QUA allows to comfortably place any code sequence in a macro to be tested separately and reused easily.
We plot an example of Rabi-Chevron map in Fig. 4a (code not shown here), together with a resulting Ramsey-Chevron map in Fig. 4b, courtesy of Quantum Simulation Group, at the Lawrence Livermore National Laboratory. To obtain the latter, we sweep delay and detuning and show average state probability using color. Thanks to ultra-fast loops running on the PPU and the low latency of the active reset (~220 ns for OPX+), this map took less than 2 minutes to extract.
Two other basic characterization protocols we will use as examples are T1 and T2 (echo) measurements, which we sketch in Fig. 5. These are generally measured to complete the understanding of coherence times for any given qubit.

As shown in the QUA codes below, both sequences are coded in less than 10 lines, written as easily as pseudocode. Such instructions can be extended to work simultaneously on any qubit number with just one extra line for a for loop, showcasing how seamless scaling up can be with the OPX platform. The fitting for the retrieval of the coherence times can be done directly on the stream processing, without involving the lab PC in calculations.
# T1 QUA code example
with for_(n, 0, n < n_avg, n + 1): #Averaging loop
with for_(*from_array(tau, taus)): #Delay loop
play("x180", "qubit")
wait(tau, "qubit")
align("qubit", "resonator")
measure(..., I, Q),
active_reset("qubit")
# T2-echo QUA code example
with for_(n, 0, n < n_avg, n + 1): #Averaging loop
with for_(*from_array(tau, taus)): #Delay loop
play("x90", "qubit")
wait(tau, "qubit")
play("x180", "qubit")
wait(tau, "qubit")
play("x90", "qubit")
align("qubit", "resonator")
measure(..., I, Q),
active_reset("qubit")
This closes our section on basic characterization for superconducting qubit. In the next section we will see two more advanced characterization protocols based on Randomized Benchmarking, and more advanced sequences further down.
An honorable mention on characterization techniques goes to the common protocols for readout optimization. Thanks to the fast runtimes of the OPX+, we can design many semi-automated procedures to optimize every component of an experiment. On our github, you can find example codes for readout optimization of frequency, amplitude, duration and integration weights, to make sure your readout always runs with the maximum possible fidelity.
Randomized benchmarking (RB) is one of the go-to experiments to show the quality of operation of a QPU, measuring the average gate error rate. RB requires us to iterate a random sequence of randomly sampled gates. Due to its intrinsic random nature and its loops, RB-like protocols heavily benefit from a controller able to generate pulses on the fly according to a specified logic. In contrast, play-from-memory controllers exhibit much slower results (and thus lower fidelity). The PPU allows users to randomize and generate the sequences with the lowest latencies at the lowest level of the hardware. In the QUA code below, we show an example of how we implement single-qubit RB to run on an OPX:
# Single-Qubit Randomized Benchmarking QUA code example
with for_(m, 0, m < num_of_sequences, m + 1): # loop over the random sequences
sequence_list, inv_gate_list = generate_sequence(interleaved_gate_index=interleaved_gate_index) # Macro generate sequence
assign(depth_target, 0)
with for_(depth, 1, depth <= 2 * max_circuit_depth, depth + 1):
assign(saved_gate, sequence_list[depth])
assign(sequence_list[depth], inv_gate_list[depth - 1]) # Add inverse sequence
with if_((depth == 2) | (depth == depth_target)):
with for_(n, 0, n < n_avg, n + 1): # Averaging loop
active_reset("qubit")
align("resonator", "qubit")
with strict_timing_(): # play with no gaps
play_sequence(sequence_list, depth)
align("qubit", "resonator")
state, I, Q = readout_macro(threshold=ge_threshold, state=state, I=I, Q=Q)
if state_discrimination: # stream results
save(state, state_st)
else:
save(I, I_st)
save(Q, Q_st)
assign(depth_target, depth_target + 2 * delta_clifford)
assign(sequence_list[depth], saved_gate)
save(m, m_st) # counter for progress bar
with stream_processing():
m_st.save("iteration")
if state_discrimination:
# during the sequence, the stream processor calculates averages, state discriminations, and all other necessary
state_st.boolean_to_int().buffer(n_avg).map(FUNCTIONS.average()).buffer(max_circuit_depth / delta_clifford + 1 ).buffer(num_of_sequences).save("state")
state_st.boolean_to_int().buffer(n_avg).map(FUNCTIONS.average()).buffer( max_circuit_depth / delta_clifford + 1 ).average().save("state_avg")
else:
I_st.buffer(n_avg).map(FUNCTIONS.average()).buffer(max_circuit_depth / delta_clifford + 1).buffer(num_of_sequences).save("I")
Q_st.buffer(n_avg).map(FUNCTIONS.average()).buffer(max_circuit_depth / delta_clifford + 1).buffer(num_of_sequences).save("Q")
I_st.buffer(n_avg).map(FUNCTIONS.average()).buffer(max_circuit_depth / delta_clifford + 1).average().save("I_avg")
Q_st.buffer(n_avg).map(FUNCTIONS.average()).buffer(max_circuit_depth / delta_clifford + 1).average().save("Q_avg")
We do not show the macros generate_sequence() and play_sequence() as they are just trivial strings of assign() and play() commands, respectively. In generate_sequence(), a rand command gets a random number generator contained in the PPU to spit the necessary numbers for the generation (assign(step, rand.rand_int(24))).
In respect to previous examples, we also see the play_sequence() macro running in a strict_timing() section, which is to say that the PPU will ensure this runs without any unwarranted gaps between pulses. In Fig. 6 we show how the circuit is built and what a resulting single-qubit RB looks like for a superconducting qubit controlled via OPX+.
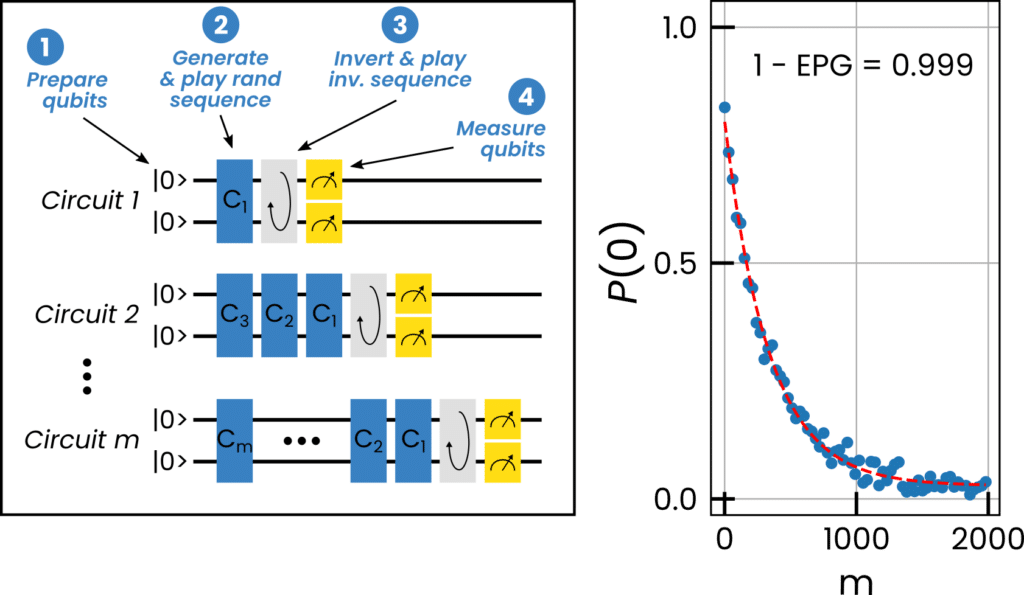
Lastly, it is worth noting that the stream processing happens during the sequence on the separate ARM processor of the OPX. The stream processor calculates averages, state discriminations, and all else necessary to feed the lab PC directly with what is relevant to plot.
Randomized benchmarking is also widely used to characterize the average error rate for two-qubit gates. Two-qubit RB works similarly to the single-qubit case shown above, except it has to include both single- and two-qubit gate sets. Thus, the four elements needed (see Fig. 6a) are single-qubit universal gate set, two-qubits universal gate set, initialization and measurement, shown in QUA macros below:
# Components macro of two-qubits Randomized Benchmarking QUA Code
# Single-Qubit Gates
def bake_phased_xz(baker: Baking, q, x, z, a):
qe = qubit0_qe if q == 0 else qubit1_qe
pulse = qubit0_x_pulse if q == 0 else qubit1_x_pulse
baker.frame_rotation_2pi(-a, qe)
baker.play(pulse, qe, amp=x)
baker.frame_rotation_2pi(a + z, qe)
# Two-Qubits Gates
def bake_cz(baker: Baking, q1, q2):
q1_xy_elem = f"qubit{q1}_xy"
q2_xy_elem = f"qubit{q2}_xy"
q2_z_elem = f"qubit{q2}_z"
baker.play("cz", q2_z_elem)
baker.align()
baker.frame_rotation_2pi(qubit1_frame_updt, q2_xy_elem)
baker.frame_rotation_2pi(qubit2_frame_updt, q1_xy_elem)
baker.align()
# Initialization/Preparation
def prep(baker: Baking, q1, q2):
measure('readout', 'resonator’, ..., I_reset))
align('qubit', 'resonator’)
play('x180', 'qubit', condition = (I_reset > threshold_g))
# Measurement/Readout
def meas():
rr0_name = f"qubit0_rr"
rr1_name = f"qubit1_rr"
Iq0 = declare(fixed)
Iq1 = declare(fixed)
measure("readout", rr0_name, None, demod.full("iw",Iq0))
measure("readout", rr1_name, None, demod.full("iw",Iq1))
return Iq0 > 0, Iq1 > 0
Once we have these elements, two-qubit RB is a randomized generation of very long sequences with many variations. For ease of use we wrapped all of that in a simple TwoQubitRb() QUA command for everyone to use. Thus, the entire code looks like the following, it compiles in less than a second and runs in just a few.
# Actual two-qubits Randomized Benchmarking QUA code
rb = TwoQubitRb(local_config, bake_phased_xz, {"CZ": bake_cz}, prep, meas, verify_gen=True)
res = rb.run(qmm, seq_depths=[10, 100, 200, 500, 1000], num_repeats=100, num_avgs=10000)
In Fig. 7 we show an animation of the oscilloscope view looking at the signals out of the OPX running this code. The animation is heavily slowed down to allow to see the change of pulses, and shows flux and measurement channels, followed by the I quadrature for both qubits.
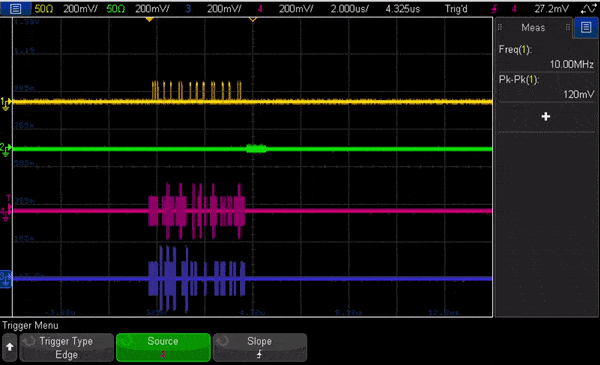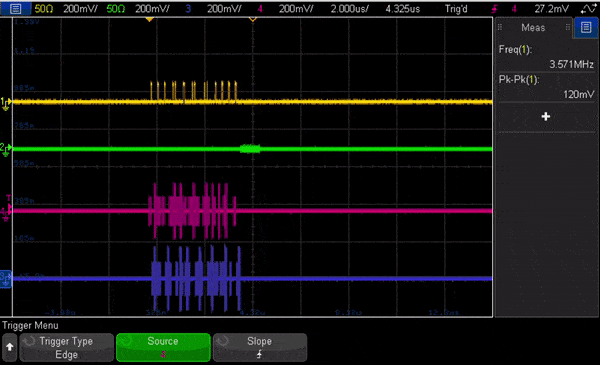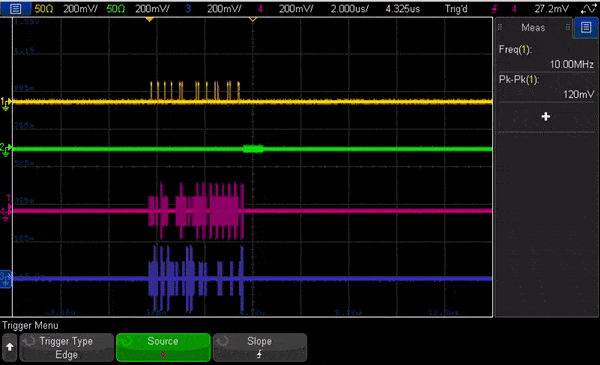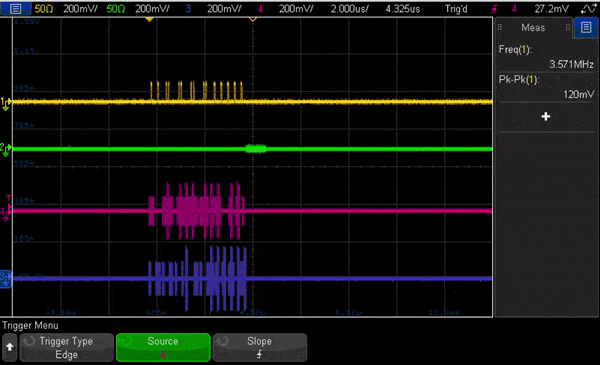
Here is a short video on two-qubit RB:
The PPU’s unique architecture has been designed for measurement-based real-time feedback. All operations, pulse generation and manipulation, logic or other, can be done based on real-time measurement results. This is a prerequisite for many advanced quantum error correction schemes, as we will see in a later example. For now, we take a simpler protocol like active reset, and we show how easy it is to implement with QUA and OPX.
The vast majority of quantum sequences start with an initialization step, to bring the qubit back to a known stable state. This is often done by waiting e.g. 10 times the qubit’s thermalization time (as in the first code on this page). This works for small QPUs, but it quickly limits us when working with many qubits or very high fidelities. Instead, we can actively reset the qubit (and any number of qubits simultaneously) thanks to real-time measurement-based feedback capability of the PPU:
# Active Reset Macro QUA code example
def basic_active_reset(threshold):
measure("readout", "resonator", None, demod.full("cos", I), demod.full("sin", Q))
play("x180", "qubit", condition = I>threshold)
Here we defined a macro for a basic active reset, which just requires a precalibrated threshold, measures the qubit and then plays a pi-pulse conditionally on the qubit’s state being excited. Simple, yet very powerful. This takes just ~200 ns to perform on an OPX+, reducing time waste and increasing fidelities (read more on our blog).
We can improve further if time is not too critical. An active reset can be coded as a repeat-until-success (RUS) protocol that keeps measuring and playing conditional π-pulses until the state is recorded at a much higher threshold. In this we can essentially choose the initialization fidelity we require, and the trade-off is just initialization time (still, this often sums up to be less than thermalization reset time). In Fig. 8 we show the flowcharts of these protocols with an example distribution.
Fig. 8 – Schematics of two active reset protocols: standard one-shot active reset and repeat-until-success (RUS) reset. On the right, their relative thresholding mechanisms explained using probability distributions.
We can promptly define a macro for RUS reset in QUA with the following code:
# Repeat-until-success Active Reset QUA code example
def RUS_active_reset(thre_g, thre_e):
measure("readout", "resonator", None, demod.full("cos", I), demod.full("sin", Q))
with while_(I>thre_g):
play("x180", "qubit", condition = I>thre_e)
measure("readout", "resonator", None, demod.full("cos", I), demod.full("sin", Q),)
Very simple to write, yet very tricky to perform. The controller must be able to handle sequences of an unknown duration (non-deterministic) and respond to changes and measurements within hundreds of nanoseconds. RUS protocols are a powerful arsenal which is still underrepresented for what they provide, and can jumpstart fidelities and multi-qubit operations.
Although RUS reset could possibly improve initialization fidelities of even two nines, this is yet not the best that can be done with an OPX. Since all variables of the sequence live on the PPU and can be used and modified during the sequence nothing is preventing changing even the thresholds and distributions dynamically, the more measurements we obtain. Dynamic RUS resets are the only way forward for initializing thousands of qubits with high fidelity.
Yet, initialization is not the only place where we can lose fidelity. Every parameter of the physical system under study drifts with time (amplitudes, frequency, etc.). This is the perfect setting to discuss another powerful feature enabled by ultra-fast measurement-based feedback is what we call embedded calibrations.
Embedded calibrations are fine tuning of calibrated parameters that can be performed during the sequence, mid-shot or mid-circuit. We will take as example the frequency of the qubit drive, but a similar code can be written for any other relevant parameter.
The natural frequency of the qubit drifts in time due to imperfections and environment interactions. The further it is from our drive frequency, the lower the operational fidelity. To always work at maximum fidelity throughout our quantum circuit we must be able to track the frequency drifts and correct our drive accordingly. With the OPX this can be done easily and mid-circuit. Here is an example of how we write such tracking in QUA using the two-Ramsey-points method (you can read more on our blog).
# Frequency tracking QUA code example
with for_(n, 0, n < 2**any_power_of_two, n + 1):
# Assign freq left and right of resonance & prepare qubit
with for_(idx, 0, idx < 2, idx + 1):
assign(f, f_resonance + minus_or_plus_delta[idx])
RUS_active_reset("qubit") # RUS macro, I_g > 3 sigma
# Perform Ramsey sequence with detuning
update_frequency("qubit", f)
play("x90", "qubit")
wait(dephasing_time, "qubit")
play("x90", "qubit")
align("qubit", rr)
# Perform measurement and real-time state discrimination
measure("readout", "resonator", ... , I )
assign(result, I > thre_g)
assign(two_point_vec[idx], two_point_vec[idx] + (Cast.to_fixed(result) >> any_power_of_two)) # Calculate and Correct frequency drift
assign(correction, Cast.mul_int_by_fixed(scale_factor,(two_point_vec[0] - two_point_vec[1])))
assign(f_resonance, f_resonance - correction)
This protocol allows to quickly check the qubit resonance frequency and correct the drive. In Fig. 9 we show two example results from this protocol. The first, Fig. 9a, is an ultra-fine stabilization of three qubits on a QuantWare QPU. In this case a longer latency is traded for an extremely narrow frequency distribution. The second, Fig. 9b courtesy of the Schuster lab at Stanford University, shows the correction applied to produce hours-long stable measurements.
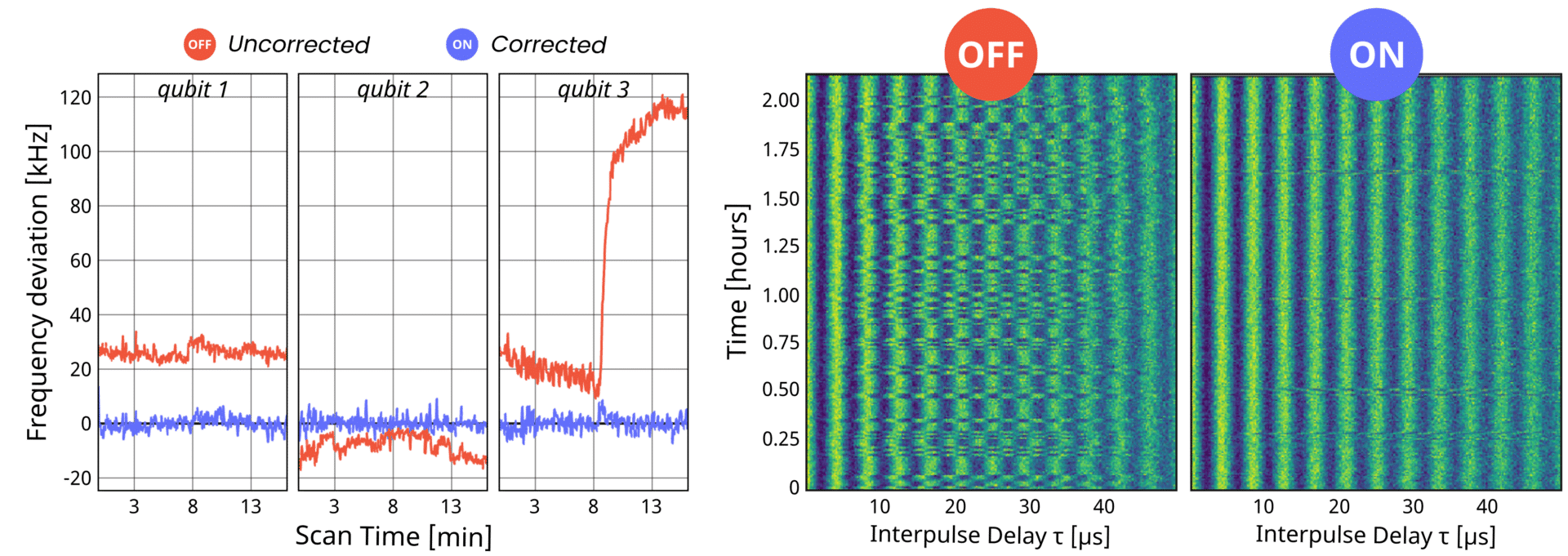
Such measurement-based feedback codes are just example for the much broader and so critical capability offered by the OPX family of controllers. In the next section we will showcase a couple of advanced examples that not only require mid-circuit measurements-based feedback as a starting point, but also push the limits of today’s technology.
Quantum error-correction is a great example demonstrating the integration of many of the benefits of Quantum Machines’ control suite. Here we show an example of how you can easily implement a 3-qubit bit-flip code on a Superconducting qubit device with the OPX.
We refer again to Fig. 1 above for the experimental setup. Four transmon qubits are controlled (we will need five for this code to run, but extending the schematics is trivial) using microwave signals generated by the OPX+ and Octave combo, for XY control. Flux bias signals are generated directly by four additional analog output channels of the OPXs+, for Z control. These can also be controlled via QDAC-II for lower noise floor on DC and low-frequency controls, or even via a combination of OPXs and QDACs.
Each qubit is coupled to a readout resonator and all four resonators are coupled to the same transmission line for multiplexed readout. The transmission line is probed using another microwave signal which is IQ modulated (with Octave) by two analog output channels of an OPX+ and measured after down-conversion by the OPX+ analog input channel.
Fig. 10 below shows the 3-qubit bit-flip code circuit. A logical qubit state |ψ⟩=α|0⟩+β|1⟩ is encoded using three physical qubits in the state α|000⟩+β|111⟩. If the first qubit was prepared in the original state |ψ⟩, then this can be done by performing two CNOT gates as shown in the encoding stage of the circuit in the figure. The idea of the 3-qubit bit-flip code is that a single bit flip in the encoded stage can be detected by measuring and tracking the parity of two pairs of qubits (repeat error tracking stage of the circuit in Fig. 10). This can be repeated to track the bit-flips during some time, after which a correction is applied to the three qubits according to the error tracking results (correction stage in Fig. 10). Finally, the state is decoded back to the state of a single physical qubit.
The parity measurements can be done by employing two more ancilla qubits initialized in the |0⟩ state before every measurement sequence. To measure the parity of a pair of qubits, say qubit 1 and 2, one CNOT gate is applied to qubit 1, and the ancilla qubit, and one CNOT gate is applied to qubit 2 and the same ancilla. This entangles the parity of the two qubits with the state of the ancilla, which can then be measured to determine the parity.
Fig. 10 – Circuit for a 3-qubit error correction code. Two ancilla qubits are used to enable both error detection and correction. |ψ⟩L is the logical qubit, expressed in the extended Hilbert space.
From the control perspective, running such a protocol is very demanding as it requires certain capabilities such as:
Let us now see how this can be implemented in QUA to run on an OPX controller:
# 3-qubits Bit Flip code QUA example
# Preparation
reset_qubits(drive_elements, readout_elements)
play('pi/2', 'q0_xy')
# Encoding
CNOT('q0_xy', 'q1_xy')
CNOT('q0_xy', 'q2_xy')
# Error tracking
with for_(i, 0, i < repetitions, i+1):
CNOT('q0_xy', 'a0_xy')
CNOT('q1_xy', 'a0_xy')
CNOT('q1_xy', 'a1_xy')
CNOT('q2_xy', 'a1_xy')
#macro for simultaneous measurements (provides ancilla states)
measure_states(['a0_resonator', 'a1_resonator'], an_states, [0,0])
save_vector(an_states, 'states')
with if_(an_states[0]==0 & an_states[1]==1):
play('pi', 'a1_xy')
assign(flips[2], ~flips[2]) # flips = parity of number of flips
with if_(an_states[0]==1 & an_states[1]==0):
play('pi', 'a0_xy')
assign(flips[0], ~flips[0])
with if_(an_states[0]==1 & an_states[1]==1):
play('pi', 'a0_xy')
play('pi', 'a1_xy')
assign(flips[1], ~flips[1])
save_vector(flips, 'all_ground')
# Error correction
with if_(flips[0]):
play('pi', 'q0_xy')
with if_(flips[1]):
play('pi', 'q1_xy')
with if_(flips[2]):
play('pi', 'q2_xy')
# Decoding
CNOT('q0_xy', 'q1_xy')
CNOT('q0_xy', 'q2_xy')
Following the components of Fig. 10, the QUA code starts with initialization (comfortably placed in the macro reset_qubits(), as seen before on this page). After the qubits are in the ground state, we apply a pi/2-pulse to the first data qubit to be ready to start the tracking protocol.
The encoding step sees entanglement of the data qubit with the other two using CNOTs. Then, the error tracking phase runs inside a for loop which repeats blocks of CNOT gates followed by measurements, from which an error syndrome can be extracted. This step requires real-time processing on mid-circuit measurements, and its operational latency is critical since it limits the correction bandwidth.
If an error is detected, one of the conditional statements applies the appropriate recovery gate. The actual waveforms required to perform CNOT gates vary between quantum computer implementations, so we have wrapped it within another macro, which is constructed and tested separately.
This implementation of a bit-flip quantum error correction is a prime example of how quantum circuits which are adaptive, include conditional operations based on mid-circuit measurement results, can have an edge over non-adaptive ones. Adaptive circuits and its classical operations offer richer computational capabilities and also non-locality of operation. One case study showing non-locality is quantum teleportation.
Quantum teleportation is well known for communication and quantum key distribution protocols, but it is also very useful for superconducting qubit chips to move a state from a qubit to a distant other. The common way this is done is to use a series of SWAP gates, but the number of gates scales linearly with the distance, quickly reaching a maximum given a limited coherence. A teleportation protocol, on the other hand, has only a fixed number of gates and operation for an arbitrary distance, provided operations can be done in parallel on many qubits. In Fig. 11 we show an example circuit for a distance 6 teleportation, very feasible with an OPX controller.
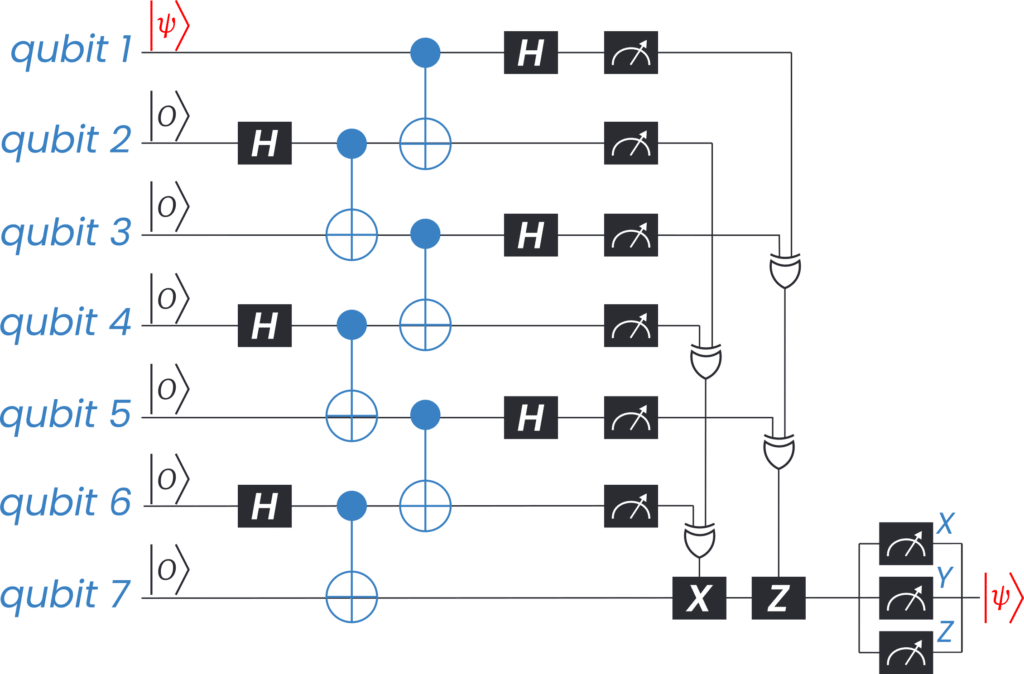
Such a protocol really stresses the controller requiring fast gates, simultaneous mid-circuit measurements and response with ultra-fast latency based on aggregated results. We leave it to the reader to try and imagine how this can be written in QUA, and we encourage to write us a proposed code so we can share ideas and show you the results first-hand.
The ease of use of QUA and the capabilities of the OPX and its PPU allow to write advanced sequences such as this in a matter of minutes. It is very common to see qubit labs performing all calibrations, characterization and all advanced quantum circuits in mind, in just the first few days of operation. Have a look at this blog post to see what a typical 48 hours installation looks like.
I hope this dive into examples for superconducting qubits was interesting. I am sure now you have more questions than before starting to read. So it is a good time to contact us for a virtual demo, where you can ask us live questions on how to perform the most advanced sequences you have in mind.
Here is the link, so what are you waiting for?
“The Quantum Machines OPX control system has been an enabling technology for our research. It provides unparalleled flexibility and ease of use for experiments requiring real-time quantum feedforward control. With the integrated high-resolution time tagging, this platform is a no-brainer for advanced quantum networking experiments.”

“My group is completely satisfied with the multiple OPX systems we’ve purchased. Qubit bring-up is fast and easy, as is optimization of high-fidelity microwave and z-pulse gates. The technical support team at Quantum Machines is outstanding.”

“QM’s chip packaging solutions are exquisite pieces of engineering that have enhanced our resonator Q-factors to as much as 200 million. It is clearly a very highly engineered product that I’m sure will be widely adopted in the field.”

"Thanks to the super-fast on-board data processing of the OPX we could resolve the nonlinear phenomena of our superconducting quantum circuits. With conventional AWGs and electronics this would have taken an impractical long time. The OPX is extremely easy to operate and substantially changes the paradigm of data acquisition and analysis procedures in quantum labs."

“We were extremely surprised by the flexibility that OPX offers and by how much easier it makes our experiments. Moreover, OPX provides extreme speed-ups. No more frustration due to long waiting times for unwanted results!”

“Incorporating the OPX+ in our measurement instruments allowed us to set up time-domain measurements in minutes, seriously speeding up our sample characterization process.
With the provided extensive live online help we get the support from QM's experts to further debug any problems arising during measurements. With QM support Qilimanjaro can deliver their differential Analog Quantum Computers based on superconducting qubit technology.”

”QM's control electronics provide the best real-time features along with an intuitive and well-documented programming interface. At TII, we successfully controlled a 25-q chip and conducted multiplexed characterization of all qubits using QM’s OPX and Octave. What we appreciate most, however, is the QM’s unwavering support and commitment to helping us achieve our targets, even going so far as to send some of their best scientists when needed.”

“OPX has been a powerful enabler in our lab, helping us quickly characterize the performance of our recently discovered qubits. The hardware removes time wasted in uploading and waiting during pulse programming. QUA has substantially reduced the complexity of writing quantum protocols, allowing us to code dynamical decoupling and RB sequences in just a few lines. It remarkably saves our time in optimizing the processes and visualizing the results, allowing us to focus more on understanding the physics of our new qubits.” See case study >>
"Using the OPX has been simplifying our work in many respects due to the intuitive implementation of sequences within QUA. In addition, the support by QM helped us debugging possible issues with swift responses and an easy and informal way of getting in touch over Discord.”

"Writing our experiments [with QUA] is easy and intuitive, and we can now focus on the physics instead. In two days we had brought up our (6-q) chip completely, calibrated all parameters, and wrote the pulse sequence of our final experiment."

"OPX played a crucial role in our advanced quantum experiments. This platform is the most flexible and user-friendly system in our lab. It saved us a significant amount of time, enabling us to concentrate on quantum science and make progress much faster compared to writing our own code. Furthermore, the Quantum Machines customer success team has been extremely helpful in addressing our needs and maximizing the solution's full potential."

"Quantum Machines' OPX played a key role in our roadmap. It enabled us to get the best control electronics out there [FPGA] without having to learn how to program them. QM provides a very scalable, very easy to use and very powerful hardware, which allows us to focus on the quantum science."

“QCage integrates seamlessly into our workflow of preparing and loading QPUs and supports higher throughput in our lab. Our research directly benefits from QCage's innovative design and engineering.”

“QM's chip packaging solutions are exquisite pieces of engineering that have enhanced our resonator Q-factors to as much as 200 million. It is clearly a very highly engineered product that I am sure will be widely adopted in our field.”
“Developing a functional qubit control electronic system absorbs a PhD-student full time at least for two years. QM’S Quantum Orchestration Platform allowed us set up experiments for full qubit characterization in 2-3 days with an undergraduate summer school student.”
“Efficiently controlling multiple frequency-tunable transmon qubits can be achieved with QM's OPX and QDevil's QDAC. QDAC's high-precision and low-noise bias voltage ensures accurate qubit frequency control without compromising coherence times, while QM's OPX offers advanced control solutions that are user-friendly and require minimal technical expertise. I highly recommend using OPX and QDAC together to streamline your lab processes and advance your quantum computing research.”

“QOP is our main tool when doing error correction. It provides us with very fast feedback. It enabled us to perform advanced procedures … in a very short time. We could just purchase the technology that is tailor-made for… that we want to use.”

“We are very pleased with the Quantum Orchestration Platform (QOP) control solution. It’s remarkably easy to use, reliable, and flexible, supporting our advanced quantum research needs. The QOP dramatically expedites our research. The Quantum Machines customer success team has been instrumental in addressing all our needs to help us to maximize the full potential of the solution. We already use two systems and strongly recommend it.”
“The OPX makes it a breeze to develop from scratch a brand-new superconducting qubit capability. Getting started is straightforward, the coding is easy, and the customer support is fantastic! The OPX reduces the potential barrier to progress and is also well suited for teaching.”

“Having tried several instruments in the past, I am very impressed by Quantum Machines' OPX. It finally removes the need for us to develop any skills in FPGA programming while still benefiting from advanced FPGA capabilities in our experiments.”

“With the OPX we were able to reduce the cost of infrastructure development from a few weeks to a few days, without any need to directly program the FPGA.”

“I must say I'm very happy with QM's Quantum Orchestration Platform. It's the single most reliable piece of equipment I've got in the lab. I operate it remotely and never had any problems. I strongly recommend the OPX and the QOP to my colleagues. It is by far the simplest way to do qubit physics.”

“It is a pleasure to work with Quantum Machines, which results in enjoyable interactions and a fast pace to getting actual results. The Quantum Orchestration Platform (QOP) has been easy to use and very powerful, but we are still just scratching the surface of its full capabilities!”

“The OPX+ has allowed us to tune up complex multi-qubit measurements with multiplexed control and readout signals for studying quasiparticle poisoning and correlated errors in superconducting qubit arrays. The on-board processing has been quite useful for analyzing qubit data streams on the fly.”
Have a specific experiment in mind and wondering about the best quantum control and electronics setup?
Want to see what our quantum control and cryogenic electronics solutions can do for your qubits?