Quantum networks are one of the most spectacular endeavors towards a future based on quantum technologies, with advancements promised for quantum photonic computing, communication, metrology, and many more [1]. One fundamental building block for quantum networks is the ability to generate high-quality quantum entanglement shared between remote nodes while keeping unavoidable errors and sources of decoherence in check.
One way to purify entanglement is entanglement distillation [2], which offers a trade-off of many not-too-impure entangled states with fewer high-fidelity ones. This protocol is extremely promising in increasing fidelity via local operations, but it has demanding experimental requirements and calls for complex control systems with real-time capabilities. Such demands have harshly limited its experimental explorations, producing strong friction for the entire field.
The groundbreaking work from Kalb et al. [3] was the first demonstration of entanglement distillation on remote electron-nuclear 2-qubit nodes (NV center qubits), which include all elements of a rudimentary but practical quantum photonics network (communication qubits and memory qubits). By combining generation, storage, and processing of high-fidelity distilled entangled states, the authors paved the way for the upscaling that quantum networks needed to unlock their full potential.
Such outstanding demonstration resulted from a complex and carefully orchestrated protocol, a constellation of advanced instruments, all meticulously tuned and timed for flawless operation at the shortest timescales. Various components are used to produce the intricate protocol shown in Fig. 1, including acousto-optical modulators (AOMs) to provide the correct optical pulses, TCSPC electronics for time tagging and temporal filtering, AWGs and microprocessors for real-time waveform generation, and many more.
Fig. 1. a) Logical blocks diagram used by Kalb et al. [3] to demonstrate entanglement distillation on remote electron-nuclear 2-qubit nodes based on NV center qubits. Adapted from [3] with the editor’s permission. b) Legend of terms used.
OPX+ replaces many traditional tools such as AWGs, time-taggers, etc. It offers a unified FPGA-based platform optimized for quantum control that can orchestrate experiments and take measurement-based decisions dynamically and in hardware time. All the novel functionalities of the OPX+ are accessible using our easy-to-use python-based programming language, QUA, which is compiled directly to FPGA assembly. This powerful combination of quantum-dedicated hardware and intuitive software makes even the most complex experiments seem like a first-year programming exercise. To demonstrate this, let’s see how to perform the Kalb et al. [3] protocol using the Quantum Orchestration Platform.
To write any complex sequence, we first break it into manageable blocks. QUA allows us to create reusable macros and libraries. For instance, here’s how to program the NV center SSRO (single-shot readout [4]) block, a sequence that experimentalists perform on a day-to-day basis:
def SSRO(system,SSRO_threshold):
times_internal = declare(int, size=100)
counts_internal = declare(int)
play("laser", f"qubit{system}")
align(f"qubit{system}",f"laser_red_A1_{system}")
play("laser_on", f"laser_red_A1_{system}")
measure("SSRO_readout", f"qubit{system}", \
None, time_tagging.analog(times_internal, 300, \
counts_internal))
return (counts_internal < SSRO_threshold)QUA macro for running a single-shot readout sequence.
This macro defines two real-time variables (a vector to record the timestamps and an integer for the total number of counts), triggers the readout laser, opens a measurement window in the ADC input of the OPX+, and time-tags and counts the pulses generated by a photodiode. The macro returns a boolean, which is True when the number of counts is smaller than a threshold. Similar to Python, a QUA macro can accept parameters which, in this case, are the name of the system (1 or 2) and the threshold value. This lets us reuse the same macro to address different qubits.
Similar macros exist for routine protocols, such as SSRO or XY8 blocks. See below for the full QUA code, or visit our Quantum Sensing with NV center page for more on the XY8 sequences.
Having written macros for each block in the sequence, all that is left to do is program the control flow. With QUA, this is just a simple programming exercise. QUA is particularly simple when working with repeat-until-success protocols, thanks to the align() command, which we will now explore in more detail.
The sequence we are implementing is acting on two different nodes, each consisting of an NV center and a nuclear spin, or other photonic quantum computing platforms. Each node is controlled independently for most of the sequence, but we want the sub-sequences to align at certain stages so that the protocol continues only when both nodes are ready. Using traditional equipment would be challenging because of the abundance of repeat-until-success blocks, especially since we cannot predict in advance how long it will take each node to reach a checkpoint. Fig. 1 depicts these as the “wait for done” blocks.
With QUA, we synchronize sequences with a simple align(‘element_1’, ’element_2’) command. This tells the FPGA to wait on all commands addressing either element_1 or element_2 until they have both reached that part of the program. Evaluation happens in real-time, so we do not need to know in advance how long it will take either node to be ready. An example of how such synchronization will look in QUA is:
Nuclear_spin_init(1, counts1_total,a1,t1)
Nuclear_spin_init(2, counts2_total,a2,t2)
align("qubit1", "qubit2")QUA code to run initialization macros for two different nuclear qubits in parallel and then align the sequence temporally, waiting for both spins to have completed initialization.
Where Nuclear_spin_init() is a macro that initializes a memory qubit (system), composed of pulse applications and XY8 blocks.
def Nuclear_spin_init(system, total_counts,a,t):
i_internal = declare(int)
times_internal = declare(int, size=100)
counts_internal = declare(int)
frame_rotation(np.pi / 2, f"qubit{system}")
play("pi_half", f"qubit{system}")
wait(4,f"qubit{system}")
reset_frame(f"qubit{system}")
C13_pi_half_pulse(system)
wait(4, f"qubit{system}")
play("pi_half", f"qubit{system}")
wait(4, f"qubit{system}")
C13_pi_half_pulse(system)
update_frequency(f"qubit{system}",NV2_conditional_freq)
assign(total_counts, 0)
with for_(i_internal, 0, i_internal < 2, i_internal + 1):
play("pi" * amp(a), f"qubit{system}", duration=t)
measure("readout", f"qubit{system}", None, time_tagging.analog(times_internal, 300, counts_internal))
assign(total_counts,total_counts+counts_internal)
update_frequency(f"qubit{system}",NV_IF)QUA macro to initialize a nuclear spin. This macro contains other macros such as C13_pi_half_pulse(). See below for the full QUA code for the sequence.
The initialization macros Nuclear_spin_init() on the two qubits run in parallel on different cores. Thanks to the align() command, the FPGA knows that both qubits must be initialized at this point in the sequence to continue. We do not need to program ADwin microprocessors and tangle our setup further because QUA and OPX+ were made with such quantum experiments in mind.
Several steps in our example protocol call for a repeat-until-success flow. Therefore, there is no way to predict how many times the subroutine will run when beginning the experiment: maybe after one try and maybe after a thousand. We can implement this kind of flow with a simple while() statement, as we would in Python:
with while_((entangled == False) & (N < N_max)):
entangle()
assign(N,N+1)QUA Code
This executes the entanglement protocol, by running the entangle() macro until the entangled variable equals True, in a while loop that runs on the pulse processor, on hardware time. We also include a counter to keep track of the number of attempts to quit after a maximum is reached. Additionally, we know how long it took to exit the loop, which allows for phase tracking and correction, another useful feature of the OPX+.
Not only does the OPX+ enable decision-making during an experiment, it also takes care of the problem of the relative phase with no need for user intervention. It does that by generating its pulses with automatic hardware-level tracking of the phase accumulation of each output frequency. By default, all pulses are performed in the rotating frame of the qubit.
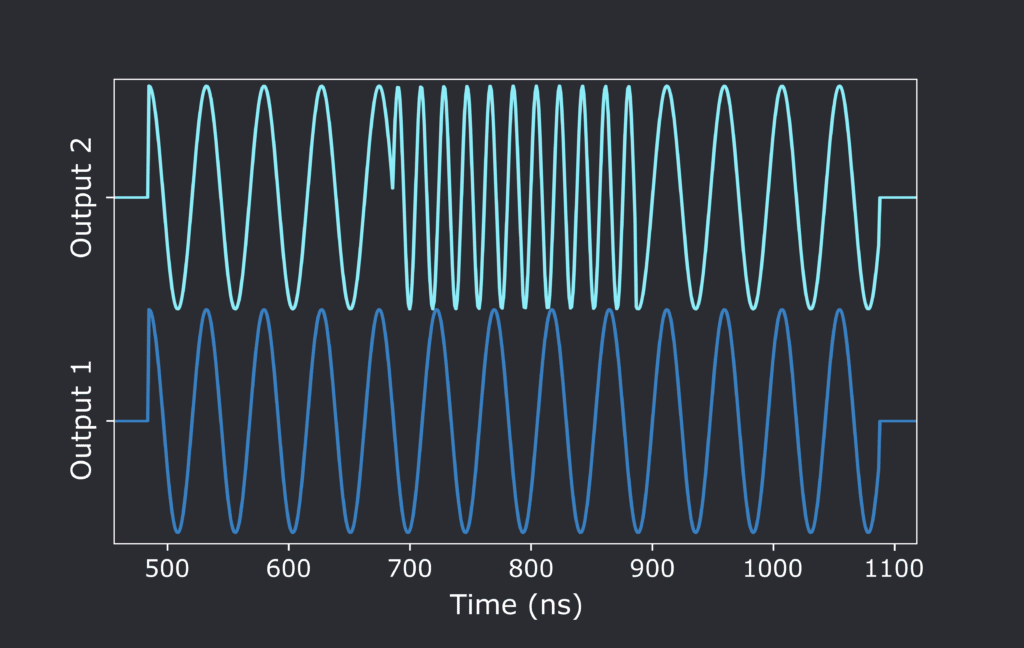
Additionally, the OPX+ allows switching between an unlimited number of frequencies while preserving the rotating frame of each tone (offering unprecedented control over the NV center qubits used). Such switching is crucial when the same output channel is driving different transitions. This is done in QUA by using the update_frequency(‘system’,‘frequency’) command as in the Nuclear_spin_init() macro you previously saw.
We can see an example of the switching by running a simple code in QUA:
With program() as Phase_Example_QUA:
reset_phase(‘output1’) ## Reset Phases
reset_phase(‘output2’)
update_frequency(‘output1’, 21168452) ## Set initial frequency
update_frequency(‘output2’, 21168452)
play(‘pi’, ‘output1’, duration = 50) ## Play pulses on outputs
play(‘pi’, ‘output2’, duration = 150)
update_frequency(‘output1’, 52849685) ## Update output1 frequency
play(‘pi’, ‘output1’, duration = 50)
update_frequency(‘output1’, 21168452) ## Update output1 frequency back
play(‘pi’, ‘output1’, duration = 50)QUA code example to show the phase tracking capabilities of the OPX+. The results of the output measurements of an OPX+ running this code are in Fig. 2.
This code plays pulses with an arbitrary frequency out of two OPX+ outputs. Then, one of the frequencies is changed and changed back. In Fig. 2, we show what an observing oscilloscope would measure at the outputs. Thanks to the OPX+ phase tracking, once the frequency of output1 is restored to the original frequency, the resulting output will still be in phase with its original twin output2. The tracking of a phase can also be reset by the reset_phase() command.
Fig. 2. Outputs of an OPX+ as measured with an oscilloscope while running the frequency update (see example QUA code in text).
OPX+ can also operate on the qubit frame, with rotations (using frame_rotation()) and complete reset of the time monitoring (using reset_frame()). Using simple commands, OPX+ offers full control over the phase. Both software and hardware are smart and intuitive, allowing you to write simple codes to run complex experiments.
The entire NV centers entanglement distillation protocol [3] runs in QUA with less than 300 lines of code. Most of this code consists of macro definitions that will be reused for other experiments and can be adapted from code snippets you will find in our open-source libraries. Once we program all basic operations into macros, the entire sequence demonstrated by Kalb et al. [3] is compressed in less than 50 lines of code, and runs with the lowest possible latencies. Additionally, as the authors suggest, the sequence can readily be improved by including steps such as active reset, which are straightforward to implement on OPX+ without complications to the experimental setup.
qmm = QuantumMachinesManager()
qm = qmm.open_qm(config)
N_max1=1000
N_max2=500
a1 = 0.2 ##amplitude for the qubit1 conditional rotations
t1 = 100 ##duration for the qubit1 conditional rotations
a2 = 0.2 ##amplitude for the qubit2 conditional rotations
t2 = 100 ##duration for the qubit2 conditional rotations
entanglement_threshold = 1
SSRO1_threshold = 1
SSRO2_threshold = 1
threshold = 1
def entangle():
times_internal = declare(int, size=100)
counts_internal = declare(int)
assign(entangled, False)
play("laser", "qubit1")
wait(4, "qubit1")
play("pi_half", "qubit1")
wait(4, "qubit1")
play("laser", "qubit2")
wait(4, "qubit2")
play("pi_half", "qubit2")
wait(4, "qubit2")
align("qubit1","qubit2","laser_red_Ey")
play("laser_pi" , "laser_red_Ey")
play("pi_plus_2ns_wait", "qubit1")
play("pi_plus_2ns_wait", "qubit2")
align("qubit1","detector")
measure("entanglement_readout", "detector", None, time_tagging.analog(times_internal, 300, counts_internal))
with if_(counts_internal > entanglement_threshold):
wait(66, "laser_red_Ey")
align("qubit1","qubit2","laser_red_Ey")
play("pi", "qubit1")
wait(70, "qubit1")
play("pi", "qubit2")
wait(70, "qubit2")
align("qubit1","qubit2","laser_red_Ey")
play("laser_pi", "laser_red_Ey")
play("pi_plus_2ns_wait", "qubit1")
play("pi_plus_2ns_wait", "qubit2")
align("detector", "qubit1")
measure("entanglement_readout", "detector", None, time_tagging.analog(times_internal, 300, counts_internal))
wait(4, "laser_red_Ey")
align("qubit1","qubit2","laser_red_Ey")
assign(entangled, counts_internal > entanglement_threshold)
def xy8_n(system,n,t):
i_internal = declare(int)
wait(t, f"qubit{system}")
xy8_block(f"qubit{system}",t)
with for_(i_internal, 0, i_internal < n - 1, i_internal + 1):
wait(2 * t, f"qubit{system}")
xy8_block(f"qubit{system}",t)
wait(t, f"qubit{system}")
def xy8_block(qubit,t):
# A single XY8 block, ends at x frame.
play("pi", qubit) # 1 X
wait(2 * t, qubit)
frame_rotation(np.pi / 2, qubit)
play("pi", qubit) # 2 Y
wait(2 * t, qubit)
reset_frame(qubit)
play("pi", qubit) # 3 X
wait(2 * t, qubit)
frame_rotation(np.pi / 2, qubit)
play("pi", qubit) # 4 Y
wait(2 * t, qubit)
play("pi", qubit) # 5 Y
wait(2 * t, qubit)
reset_frame(qubit)
play("pi", qubit) # 6 X
wait(2 * t, qubit)
frame_rotation(np.pi / 2, qubit)
play("pi", qubit) # 7 Y
wait(2 * t, qubit)
reset_frame(qubit)
play("pi", qubit) # 8 X
def C13_pi_pulse(system):
if system==1:
xy8_n(1,6,12)
else:
xy8_n(2,8, 14)
def C13_pi_half_pulse(system):
if system==1:
xy8_n(1,3, 12)
else:
xy8_n(2,4, 14)
def C13_phase_pulse(system,repetitions):
if system==1:
xy8_n(1,repetitions,12)
else:
xy8_n(2,repetitions, 14)
def Nuclear_spin_init(system, total_counts,a,t):
i_internal = declare(int)
times_internal = declare(int, size=100)
counts_internal = declare(int)
frame_rotation(np.pi / 2, f"qubit{system}")
play("pi_half", f"qubit{system}")
wait(4,f"qubit{system}")
reset_frame(f"qubit{system}")
C13_pi_half_pulse(system)
wait(4, f"qubit{system}")
play("pi_half", f"qubit{system}")
wait(4, f"qubit{system}")
C13_pi_half_pulse(system)
update_frequency(f"qubit{system}",NV2_conditional_freq)
assign(total_counts, 0)
with for_(i_internal, 0, i_internal < 2, i_internal + 1):
play("pi" * amp(a), f"qubit{system}", duration=t)
measure("readout", f"qubit{system}", None, time_tagging.analog(times_internal, 300, counts_internal))
assign(total_counts,total_counts+counts_internal)
update_frequency(f"qubit{system}",NV_IF)
def SWAP(system):
times_internal = declare(int, size=100)
counts_internal = declare(int)
C13_pi_half_pulse(system)
wait(4, f"qubit{system}")
play("pi_half", f"qubit{system}")
wait(4, f"qubit{system}")
C13_pi_half_pulse(system)
wait(4, f"qubit{system}")
frame_rotation(np.pi / 2, f"qubit{system}")
play("pi_half", f"qubit{system}")
reset_frame(f"qubit{system}")
measure("readout", f"qubit{system}", None, time_tagging.analog(times_internal, 300, counts_internal))
def purifying_gate(system):
times_internal = declare(int, size=100)
counts_internal = declare(int)
frame_rotation(np.pi / 2, f"qubit{system}")
play("pi_half", f"qubit{system}")
reset_frame(f"qubit{system}")
wait(4, f"qubit{system}")
C13_pi_half_pulse(system)
wait(4, f"qubit{system}")
play("pi_half", f"qubit{system}")
measure("readout", f"qubit{system}", None, time_tagging.analog(times_internal, 300, counts_internal))
def Charge_resonance_check():
times1 = declare(int, size=100)
counts1 = declare(int)
times2 = declare(int, size=100)
counts2 = declare(int)
assign(state_initialization, False)
play("laser", "qubit1")
play("laser", "qubit2")
align("qubit1","qubit2","laser_red_A1_1","laser_red_A1_2")
play("laser_on", "laser_red_A1_1")
play("laser_on", "laser_red_A1_2")
measure("SSRO_readout", "qubit1", None, time_tagging.analog(times1, 300, counts1))
measure("SSRO_readout", "qubit2", None, time_tagging.analog(times2, 300, counts2))
wait(200,"qubit1")
align("qubit1","qubit2","laser_red_Ey","laser_red_A1_1","laser_red_A1_2")
with if_(counts1 > threshold & counts2 > threshold):
play("laser_on", "laser_red_Ey")
play("laser_on", "laser_red_A1_1")
play("laser_on", "laser_red_A1_2")
measure("SSRO_readout", "qubit1", None, time_tagging.analog(times1, 300, counts1))
measure("SSRO_readout", "qubit2", None, time_tagging.analog(times2, 300, counts2))
with if_(counts1 > threshold & counts2 > threshold):
assign(state_initialization, True)
def SSRO(system,SSRO_threshold):
times_internal = declare(int, size=100)
counts_internal = declare(int)
play("laser", f"qubit{system}")
align(f"qubit{system}",f"laser_red_A1_{system}")
play("laser_on", f"laser_red_A1_{system}")
measure("SSRO_readout", f"qubit{system}", None, time_tagging.analog(times_internal, 300, counts_internal))
return (counts_internal < SSRO_threshold)
def Tomography_X(system,a,t,counts_total):
i_internal = declare(int)
times_internal = declare(int, size=100)
counts_internal = declare(int)
frame_rotation(np.pi / 2, f"qubit{system}")
play("pi_half", f"qubit{system}")
reset_frame(f"qubit{system}")
wait(4, f"qubit{system}")
C13_pi_half_pulse(system)
wait(4, f"qubit{system}")
play("pi_half", f"qubit{system}")
update_frequency(f"qubit{system}", NV1_conditional_freq)
play("laser", f"qubit{system}")
play("pi" * amp(a), f"qubit{system}", duration=t)
align(f"qubit{system}", f"laser_red_A1_{system}")
play("laser_on", f"laser_red_A1_{system}")
assign(counts_total, 0)
with for_(i_internal, 0, i_internal < 5, i_internal+1):
play("laser", f"qubit{system}")
play("pi" * amp(a), f"qubit{system}", duration=t)
align(f"qubit{system}", f"laser_red_A1_{system}")
play("laser_on", f"laser_red_A1_{system}")
measure("SSRO_readout", f"qubit{system}", None, time_tagging.analog(times_internal, 300, counts_internal))
assign(counts_total,counts_total+counts_internal)
update_frequency(f"qubit{system}", NV_IF)
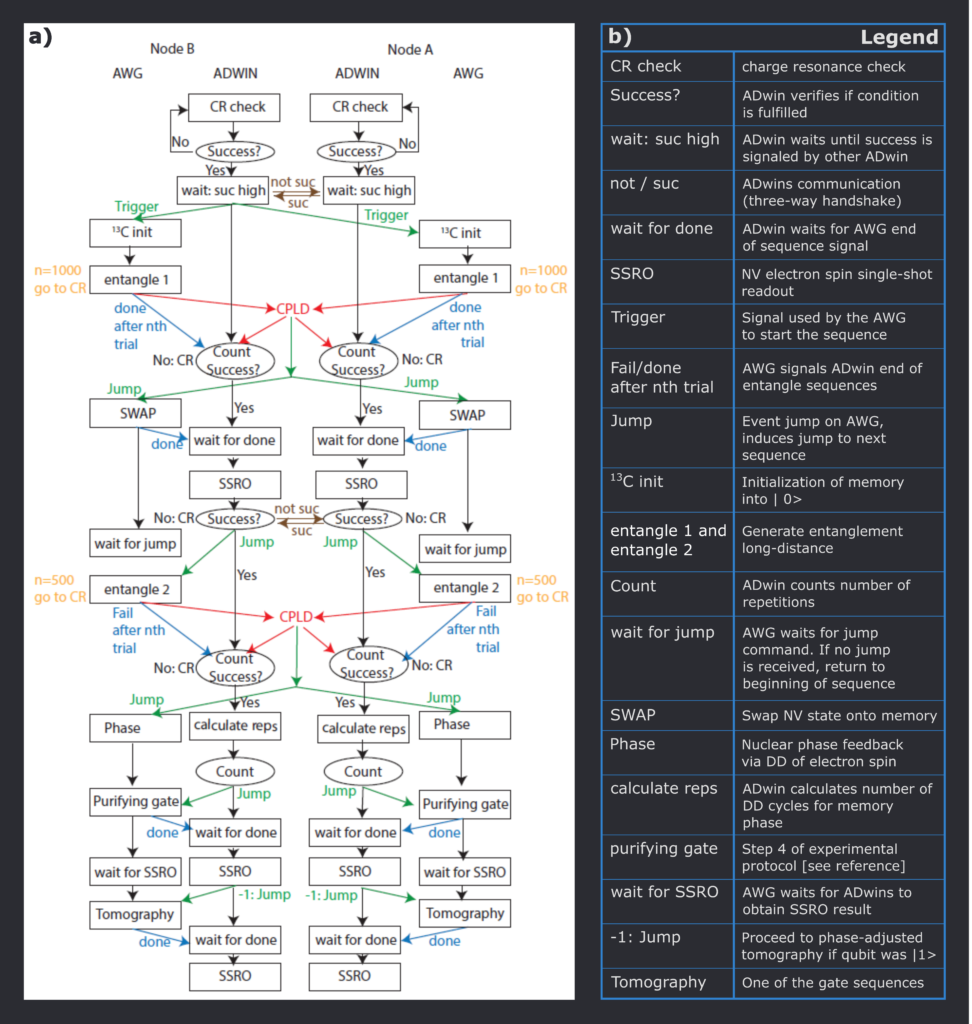
with program() as sp_ent:
times1_total = declare(int, size=100)
counts1_total = declare(int)
times2_total = declare(int, size=100)
counts2_total = declare(int)
N = declare(int)
entanglement_repetitions = declare(int)
qubit1_state0 = declare(bool, value=False)
qubit2_state0 = declare(bool, value=False)
state_initialization = declare(bool,value=False)
entangled = declare(bool,value=False)
with while_(entangled == False):
assign(qubit1_state0, False)
assign(qubit2_state0, False)
with while_((qubit1_state0 == False)|(qubit2_state0 == False)):
assign(entangled, False)
with while_(entangled == False):
assign(state_initialization, False)
with while_(state_initialization == False): ## initialization of both NV's
Charge_resonance_check()
## if successful then C13 initialization
Nuclear_spin_init(1, counts1_total,a1,t1)
Nuclear_spin_init(2, counts2_total,a2,t2)
align("qubit1", "qubit2")
## spin photon entanglement // if 1000 tries go back to the start
assign(N, 0)
with while_((entangled == False) & (N < N_max1)):
entangle()
assign(N,N+1)
## Swap the state between NV and C13
SWAP(1)
SWAP(2)
## Single Shot readout of both NV's
assign(qubit1_state0,SSRO(1,SSRO1_threshold))
assign(qubit2_state0,SSRO(2,SSRO2_threshold))
align("qubit1", "qubit2")
## spin photon entanglement 2// if 500 tries go back to the start
assign(entanglement_repetitions, N)
assign(N, 0)
assign(entangled, False)
with while_((entangled == False) & (N < N_max2)):
entangle()
assign(N,N+1)
assign(entanglement_repetitions, entanglement_repetitions + N)
C13_phase_pulse(1, entanglement_repetitions)
C13_phase_pulse(2, entanglement_repetitions)
purifying_gate(1)
purifying_gate(2)
align("qubit1","qubit2")
with if_(SSRO(1,SSRO1_threshold)):
play("pi","qubit1")
with if_(SSRO(2,SSRO2_threshold)):
play("pi","qubit2")
Tomography_X(1,a1,t1,counts1_total)
Tomography_X(2,a2,t2,counts2_total)
QUA code for running the entanglement distillation protocol demonstrated by Kalb et. al. [3]. The sequence is written to run in simulation mode.
References
[1] Kimble, H. Jeff. Nature 453.7198 (2008): 1023-1030.
[2] Bennett, C. H., et al. Physical Review A 54.5 (1996): 3824.
[3] Kalb, N., et al. Science 356.6341 (2017): 928-932.
[4] Robledo, Lucio, et al. Nature 477.7366 (2011): 574-578.
Additional resources
QM’s solution for Optically Addressable Qubits
QUA2.0 unique features with strict timing and time tagging
NV centers for Quantum Sensing
The unique features of the PPU, a controller designed for quantum experiments
Have a specific experiment in mind and wondering about the best quantum control and electronics setup?
Want to see what our quantum control and cryogenic electronics solutions can do for your qubits?