Introduction to Digital Filters 01: First things FIRst
[Written in collaboration with Gal Winer]
—
To control qubits we need to manipulate electrical signals – this is the business of quantum control. We need to generate the right signal shape, setting both its nominal voltage value and the exact time at which it occurs. This is not always an easy task because… well, life never is.
We are limited by the properties of our entire signal path, from the signal source to the Quantum Processing Unit (QPU) and back to the control hardware. This signal path will introduce delay and dispersion (i.e. frequency-dependent response), thus distorting the shape of our signals and affecting the result.
Because we use a digital processor to generate and manipulate signals, we have at our disposal the enormous flexibility and power of digital filters to condition our signal to better suit our needs. Digital filter design is a topic in and of itself, and while we can not provide a full overview here, we will cover some of the basics of digital filter usage with the Quantum Orchestration Platform (QOP).
The QOP supports two types of filters: Finite Impulse Response (FIR) and Infinite Impulse Response (IIR). FIR filters delay and correct samples using only the input signal and without consideration of the output. In other words, they perform a feed-forward operation. On the other hand, an IIR filter modifies the signal with dependence on both input and output, meaning it performs feedback as well. In this introductory post, we will only cover FIR filters.
What are digital filters anyway?
A digital filter takes signal samples, one nano-second at a time (or some other time resolution depending on the system), and performs mathematical manipulations on them. You can think about it as a long stream of numbers that can be multiplied by some (real) coefficients. In the lingo of digital signal processing, these coefficients are called “taps”. In the image below, the signal values \(x[n]\) are delayed by a single time step at each z-1 block, multiplied by the bi coefficients (the filter taps), and summed together to produce the filtered signal output values \(– y[n] \). If you don’t know the \(z^{-1}\) notation, feel free to ignore it for now (if you are really curious, it’s the z-transform representation), you need only care for the fact that it delays everything by one-time step.
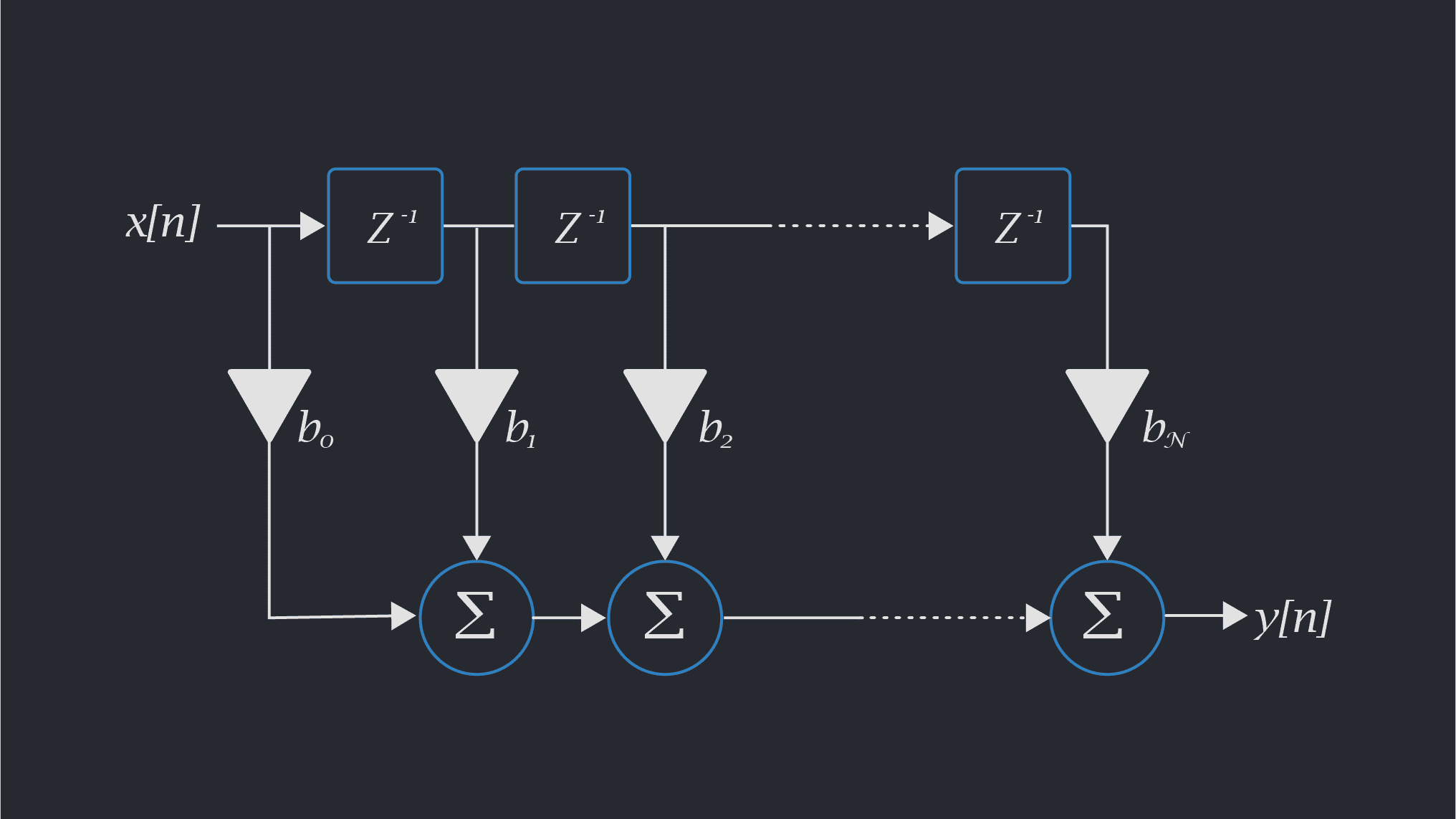
The filter in the image above modifies the signal depending only on past samples. Mathematically, filters could depend on any value of the signal – past, present, or future. However, in practice, only causal filters, which generate an output depending only on current and past signal values, may be implemented.
Filters that depend on a finite number of past signal values are called finite impulse response (FIR) filters. Filters with an infinite impulse response (IIR) may be implemented using feedback taps. This type of filter is also supported in QUA and will be discussed in a future post.
Delaying a signal using an FIR
To get a sense of how filters work, we begin by considering the pure delay (and no distortion) of a signal. To make things even simpler, suppose we want to delay a signal by an integer number of time steps, say: 5 samples. For an input \(x(t)\) we want to get \(x(t-5)\). This can be done easily by setting the 6th tap to 1 and all other taps to zero. In the diagram below you can imagine the samples going into the filter and have each sample delayed multiple \(z^{-1}\) elements, eventually to reach a non-zero tap and produce a non-zero output.
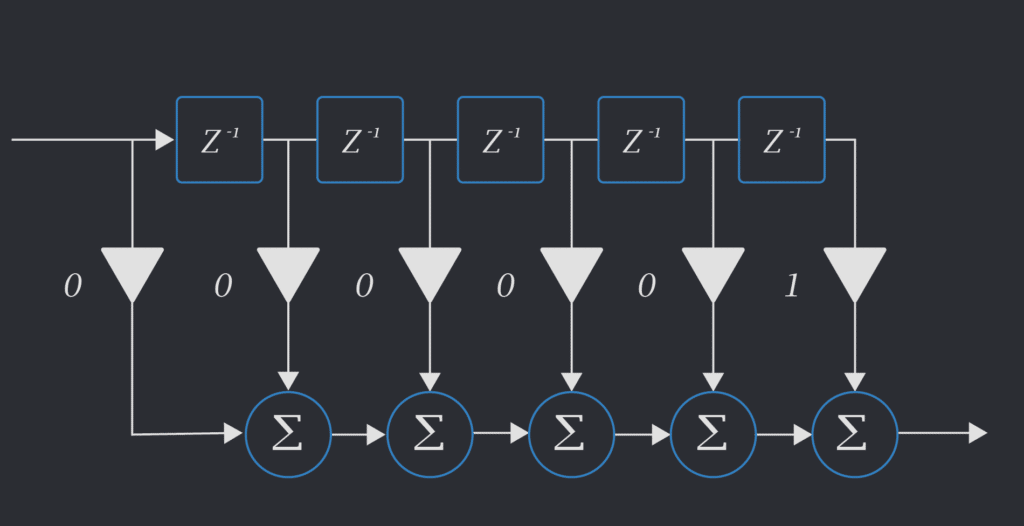
Now that we are convinced it’s pretty easy to delay a signal by an integer number of time steps, we would like to know: can we create a filter that produces a non-integer delay?
First, let’s get a bit of intuition for this. The basic idea is that we are taking advantage of our vertical resolution (in voltage) to play, at each time step, the value appropriate for the slightly (sub-ns) delayed signal. At a given time step, instead of playing the voltage appropriate for a gaussian centered at 7ns, we play the voltage appropriate for a gaussian centered at 7.2ns. However, this can only go so far because the hardware has a finite output bandwidth. Because of this, if we try to change the values too quickly those changes will be washed out by the output effectively applying a low-pass filter. So as long as we play pulses compatible with the finite bandwidth of the output (no sharp turns, please), we can introduce non-integer delay at the (analog) output of the system.
Designing a filter with non-integer delay
How would you go about designing such a filter? The theory behind filter design can be daunting as it includes some non-trivial mathematical steps. These steps are there because digital filters exist in discrete time, while we are interested in the behavior (shape) of the signal in the continuous-time domain.
We will see what this means by an example. Consider a continuous-time signal at the output of the OPX+. In general, it’s some signal of duration \(T\) which can have an output voltage between -0.5 V and 0.5V.
\(x(t) : [0: T) \rightarrow [-½,½]\)
To generate this signal we have to calculate discretely sampled voltage values. The notation used in signal processing is to have square brackets denoting discrete time. In addition we replace the continuous-time index \(t\) by the discrete-time index \(n\). Our discrete-time signal is given simply by sampling the continuous-time signal at discrete (integer) intervals.
\( x(t) \rightarrow x[n] \)
Our goal now is to manipulate \(x[n]\) using the digital filter such that the continuous-time signal \(x(t)\) is shifted by some (non-integer) constant delay \(x(t)\rightarrow x(t-\delta)\). How do we do that? The first mathematical operation needed to design our filter uses the discrete-time Fourier transform (DTFT). This is an operation that translates a discrete-time signal to its finite and continuous frequency representation. Sampling the DTFT yields the discrete Fourier transform (DFT), which is exactly the operation achieved by calling the FFT function from SciPy, MATLAB, or any of your favorite data manipulation platforms.
Filter design: to the frequency domain and back
With the benefit of hindsight, we anticipate that the design of the filter should begin in the frequency domain. To that end, we first need to translate our time domain requirement to a frequency domain representation. In the case of time-shift, this is given by Fourier transform property:
\( x(t-d) \rightarrow e^{-jd\omega}X(j\omega)\)
A filter can be represented in the frequency domain as multiplication by a known (complex) function, known as the transfer function of the filter. Therefore, our exponential prefactor is exactly the filter we want to achieve! But note, there are still some steps that need to be taken in order to translate the infinite, continuous-time filter response, \( H(j\omega)=e^{-jd\omega}\), to a finite, discrete one. First, we will sample our continuous-time filter, to get a discrete (but still infinite!) time signal. To reduce sampling errors, we will first pass the signal through a low-pass filter (this prevents the annoying signal-processing error called aliasing). The sampled function is then given in the discrete time-frequency domain as:
\(H(\theta) =e^{-jdf_s\theta}\),
Where \([0,2)\) is the frequency index of the signal (that we sampled in discrete time steps), and fs is the sampling frequency (in the case of the OPX+ that is 1 GSPS). This function has an infinite representation in the discrete-time domain which means it is not yet suitable to use as an FIR filter (which is finite in time as we recall). To overcome this, we will first transform the signal to the time domain using the Inverse Discrete-Time Fourier Transform (IDTFT)
\(h[n]=sinc(nT_s -d) \forall n \in Z \),
where \(T_s = \frac{1}{f_s}\), is our sampling interval. Now all that’s left to do is truncate the signal to the length of our filter. This means that the digital filter we wish to implement is no other than \(h[n] = sinc(nT_s – d), n\in[0,N-1]\), where Nis the number of our filter taps.
Filters in QUA: Let’s get down to business
After all this theoretical background, we’ve worked up quite an appetite. So let’s see how to implement a non-integer delay in QUA.
All we need to do is to write a function that takes a delay as input and calculates the taps:
def FIR(delay,ntaps):
return np.sinc(np.linspace(0, ntaps-1, ntaps)-delayThe ntaps parameter specifies how many frequency samples (our \(N\) from before).
Next, we place the coefficients in the qua config. The coefficients go into the analog channel section of the configuration as follows:
"analog_outputs": {
1: {
"offset": +0.0,
"filter": {"feedforward": feedforward_filter},
}, Where feedforward_filter is a list containing the calculated coefficients. The OPX+ supports up to 40 FIR taps. This can produce up to 40 ns delay but is of course much more versatile. Once a filter has been defined, any signal played to the affected output will be filtered.
Below you can see the resulting simulated shifted signal. We simulate an unshifted signal in green, a signal shifted by 7.1ns in blue and a signal shifted by 7.9 ns in orange.
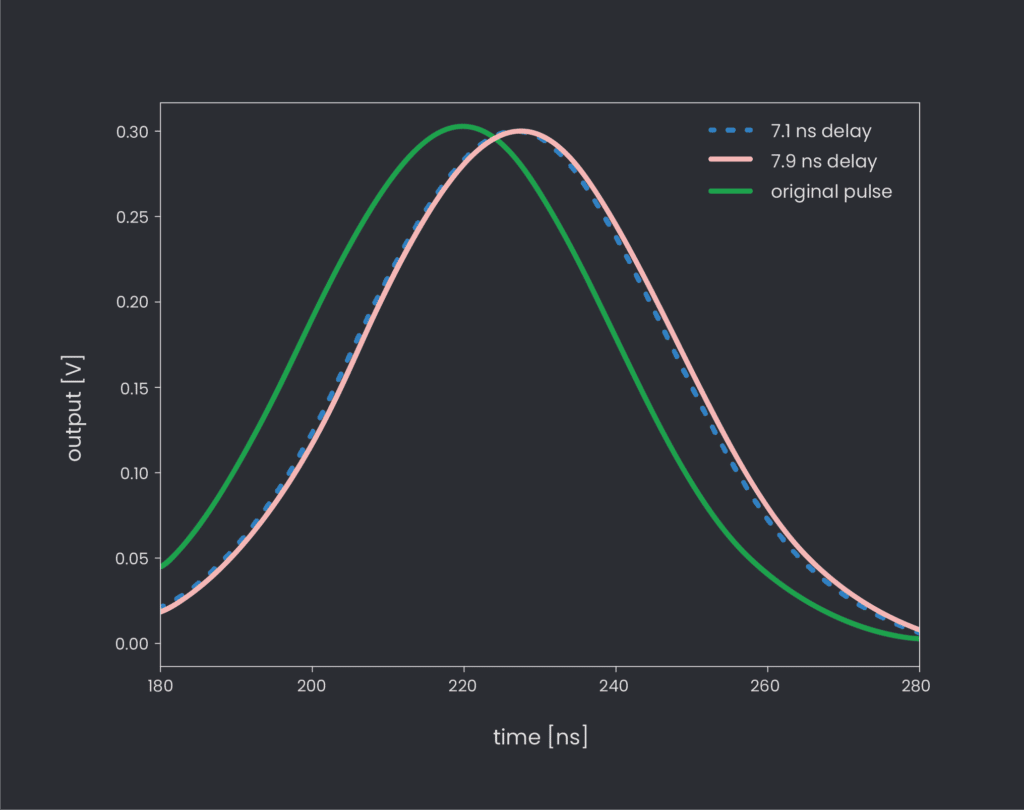
We chose to showcase these shifts on a Gaussian pulse. This is no accident. Non-integer shifts are better suited for signals with a low-frequency band. Remember that when you design a pulse to be played in hardware, there is always some limited output bandwidth to keep you under the speed limit, so signals that change too quickly aren’t suitable filter candidates anyway.
Summary
Filters are important in conditioning the pulses which a control system can create. We have only touched the tip of the iceberg here and there is a lot more that can be done. For example, correct usage of filters can allow you to correct the group dispersion (read: distortion) in a pulse due to the bandwidth of the transmission line going into your fridge and connecting your qubit to the outside world. Correct usage of this tool is therefore essential in creating high fidelity qubit operations. You can find interesting usage examples in our Github repository. In the next post in the series, we will dive deeper into filter design, learning about IIR filters and the added power they bring.
Discover More
Contact us or request a demo to learn more about OPX+ and its scaled-up version OPX1000 to better understand how these unique processor-based controllers can accelerate your research.