Paving the Path Towards Near-Term Quantum Advantage with the Quantum Orchestration Platform
Getting started in quantum computing (QC) used to be very intimidating for people without a quantum physics background. Nowadays, it seems that practically anyone can join this next revolution, given the plethora of resources available online! Like many of my fellow students, most of my training relied heavily on self-learning initiatives, especially because I wanted to work in quantum algorithms, which is the field that is by far the most anticipated by the outside world.
In fact, the development of the field in past decades has been separated into branches that closely follow the concept of abstraction layers in a computing stack. In this scenario, a person who wants to know what could be done with quantum computers, typically quantum algorithms for real-world applications, does not have to know what is happening inside the box to appreciate the interest and the complexity of this field.
This idea is far from novel. Most of us actually follow this concept every day. When you are driving a car, you do not need to know how its engine works to use it well. This is because the person who developed the car has taken good care of what’s hidden from view to save you the trouble of looking it up. However, this works well as long as your car is working, but what happens when it starts malfunctioning? If like me, you do not have the means to replace your car every time you encounter an issue, you might have to take a closer look at what’s happening inside and quickly identify how you can overcome the issues resulting from the dysfunctionality.
This intuitive idea is what motivated part of the research I conducted at Quantum Machines for a year while finishing my studies. How can we leverage the low-level pulse control and the architecture of the Quantum Orchestration Platform to enhance the performance of our current existing quantum protocols?
Within the thesis linked at the end of this blog post, you will see that the leading idea is the search for opportunities to build a common platform that can gather both quantum software engineers and hardware providers in a unified framework. From this, interesting bridges could be created for all kinds of use cases, from hardware characterization to quantum error correction.
Enabling the Realization of Variational Quantum Algorithms
The best representatives of this bridge idea are hybrid classical-quantum algorithms, considered today as the best candidates for demonstrating quantum advantage in the very near future with the most recent Quantum Processing Units – or QPUs (Did I hear you saying Eagle?).
In fact, those algorithms are specifically designed to cope with limitations inherent to the physical reality of the current hardware (e.g, coherence times, connectivity issues, gate errors) while enabling the possibility of solving concrete computational problems (e.g, combinatorial optimization, chemistry simulations, machine learning tasks, etc.).
In hybrid algos, quantum resources are exploited for computing small subroutines in a wider classical algorithm. In a nutshell, the statement of this kind of algorithm is as follows:
We know that the quantum computer is not good at computing everything, so let’s focus its use on a sufficiently small subtask where we can hope that it will give us an interesting result. This result can then be processed on a classical computer to solve our input problem.
Among the many non-trivial practicalities that emerge with these algorithms, one could wonder how the communication between classical and quantum resources is realized efficiently. Usually, the protocol consists of a loop where the classical computer iteratively calls the QPU to estimate the value of an objective function (that is a function carrying a cost indication in an optimization problem) through the execution of a “parametrized quantum circuit”. More specifically, the classical computer provides a set of real parameters, used to define the quantum circuit to be executed on the QPU, and optimizes this function through an iterative tuning of those parameters.
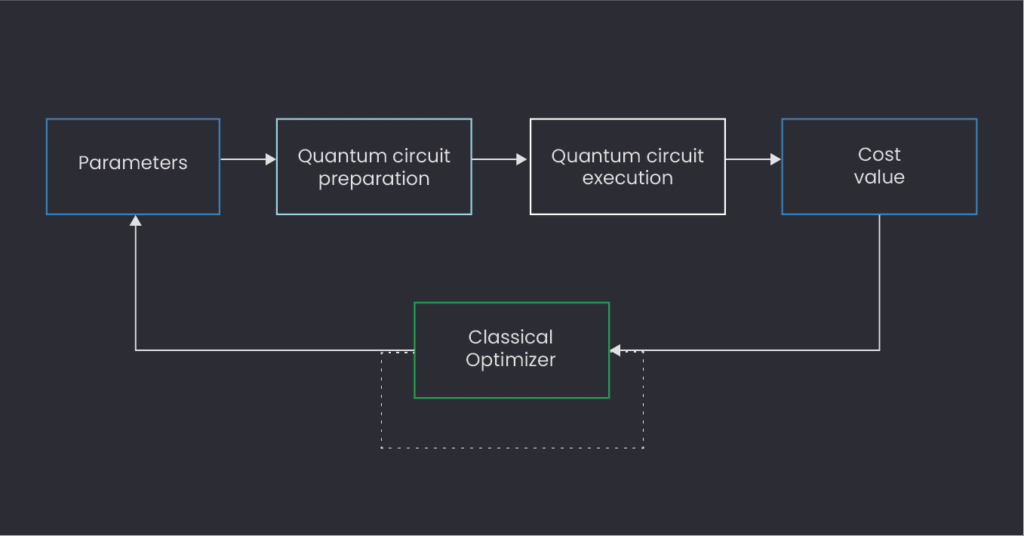
In a traditional setting, each call to the QPU results in the generation of a new job to run, involving a potential reload of the entire quantum circuit (which may contain lots of instructions and therefore take time to compile). This is rather inefficient, especially if one wants to run big programs using a few hundred qubits. With the Quantum Orchestration Platform, things can happen quite differently, and there are many options to be explored to push the boundaries of our current execution times.
A few of these currently available options are described in my thesis, and many more are yet to come in the near future, but there is one particularly well suited for running a particular variational quantum algorithm today: the Quantum Approximate Optimization Algorithm, widely known as QAOA [1].
Implementing QAOA in QUA
Introduced in 2014, this algorithm aims to provide an approximate solution to a combinatorial optimization problem, that is finding an optimal solution among a discrete and finite set of possibilities.
When I arrived at Quantum Machines over a year ago, my first task was to cast QAOA in a QUA-friendly fashion. At first glance, this sounded quite complicated, as QUA is a pulse-level programming language, whereas the only thing I knew how to handle at the time was the circuit model of quantum computing, which you can use now in God knows how many Quantum SDKs today. However, I quickly realized that QUA brought something extra to the table, something that used to be invisible when dealing only with abstract quantum gates.
Firstly, QUA is built such that it is possible to encapsulate all pulse commands into user-defined QUA functions known as macros, effectively allowing the user to write something equivalent to the circuit level with great ease, placing the quantum programmer on familiar ground. In the figure below, you can see the QUA code required to compute the QAOA circuit. Evidently, everything is quite self-contained. Note that for simplicity, we assumed that the connectivity of the hardware matches the connectivity of the graph on which we are trying to find the Maximum Cut, which is the canonical problem solved by the QAOA (for the brave, more details can be found in my thesis).
MaxCut is a very famous problem in graph theory. Essentially it’s a graph optimal partition search, and it is known to be computationally hard (it is actually NP-complete!). The fact that finding an approximate solution using a quantum computer can be done efficiently makes it a very interesting candidate for the first demonstration of quantum advantage. And indeed in 2014, QAOA was introduced as a quantum method for efficiently approximating a solution to MaxCut. Below, we show an implementation of this algorithm:
# Start running quantum circuit (repeated N_shots times)
with for_(rep, init=0, cond=rep <= N_shots, update=rep + 1):
for k in range(n): # for each qubit in the config (= node in the graph G)
Hadamard(q[k])
with for_(
b, init=0, cond=b < p, update=b + 1
): # for each block of the QAOA quantum circuit
# Cost Hamiltonian evolution: derived here specifically for MaxCut problem
for e in E: # for each edge of the graph G
e1, e2 = int(e[0]), int(e[1])
ctrl, tgt = q[e1], q[e2]
CU1(2 * γ[b], ctrl, tgt)
Rz(-γ[b], ctrl)
Rz(-γ[b], tgt)
align()
# Mixing Hamiltonian evolution
for k in range(n): # Apply X(β) rotation on each qubit
Rx(-2 * β[b], q[k])
# Measurement and state determination
for k in range(n): # Iterate over each resonator
measure("meas_pulse", rr[k], None, integration.full("integW1", I))
assign(state[k], Cast.to_int(I > th))Each gate used here is actually a macro containing a set of simple QUA instructions. A CU1 gate is typically defined for an IBM superconducting qubit device, like the ones available through the IBM cloud, which is specified here. An Rz gate is, in this case, directly related to a QUA command called frame_rotation and essentially enables you to perform what is called a virtual Z rotation [2]. For more details, you can take a look at the full code of the QAOA implementation in QUA right here.
Enhancing the Execution Workflow with the QOP Architecture
But the true power of QUA stands in its ability to enable the writing of real-time computations and subroutines that can drastically increase the performance of the algorithm at no additional cost. Say you want to add an active reset to your original algorithm. Two added lines of code to your circuit are enough, as discussed in a previous blog post. Typically for the QAOA, computing the objective function based on the measurement results obtained from the QPU is extremely easy to write in QUA. In the code snippet below, you can see an example of such cost function evaluation written in QUA for the MaxCut problem. Writing this function in QUA enables two things:
- This calculation can be done in parallel to the execution of the following quantum circuit. In fact, the cost function associated with the QAOA is a simple weighted average of the bit strings obtained by measuring all the qubits. In this form, each contribution to this average is added on the fly and is parallel to circuit execution. This means that we no longer have to wait for all results to be retrieved by the user at the end of the sampling to perform parameter optimization in the classical processor.
- We reduce the amount of data to be sent back to the classical computer by simply returning one single value, the evaluated cost function, instead of returning the entire statistics associated with our measurement series that would require post-processing.
# Cost function evaluation
for e in E: # for each edge of the graph G
e1, e2 = int(e[0]), int(e[1])
assign(w, G[e1][e2]["weight"]) # Retrieve weight associated to edge e
assign(
Cut,
Cut
+ w
* (
Cast.to_fixed(state[e1]) * (1.0 - Cast.to_fixed(state[e2]))
+ Cast.to_fixed(state[e2]) * (1.0 - Cast.to_fixed(state[e1]))
),
)
assign(Expectation_value, Expectation_value + Cut)
assign(Expectation_value, Math.div(Expectation_value, N_shots))
assign(IO1, Expectation_value)
# save(Expectation_value, "exp_value")QUA is a great tool for computing a quantum algorithm, but our story does not stop there!
It also turns out that the architecture of the QOP itself is tailor-made for the realization of those hybrid algorithms. Among the many features that it offers, one stands out as particularly suitable for the parameter update step: Input/Output (I/O) variables, marked as IO1 in the last line of the code above.
This setting allows the passing of a series of numbers from the client PC to the OPX+ without having to reload the entire program in memory. Even better, we can set up the QUA program such that each iteration of a new circuit waits for parameters to be uploaded before proceeding to the execution of the next step. We, therefore, move from the successive execution of multiple distinct jobs on the quantum computer to one single QUA program written within an infinite loop which is successively paused and resumed where circuit parameters must be updated. This works particularly well for the QAOA, as the circuit structure (the ansatz) remains unchanged across iterations. But note that we could also, on-the-fly select multiple circuit layers to be played (within a pool of subcircuits) and dynamically change the ansatz form.
In the graph below, you can see the time difference (in seconds) between the usage of I/O variables and a usual setting for a VQA, that is the relaunch of a new job each time parameters are changed. Here, the graph solely indicates the time required for the parameter update step (it excludes the runtime of the QAOA circuit, as well as the classical optimization routine).
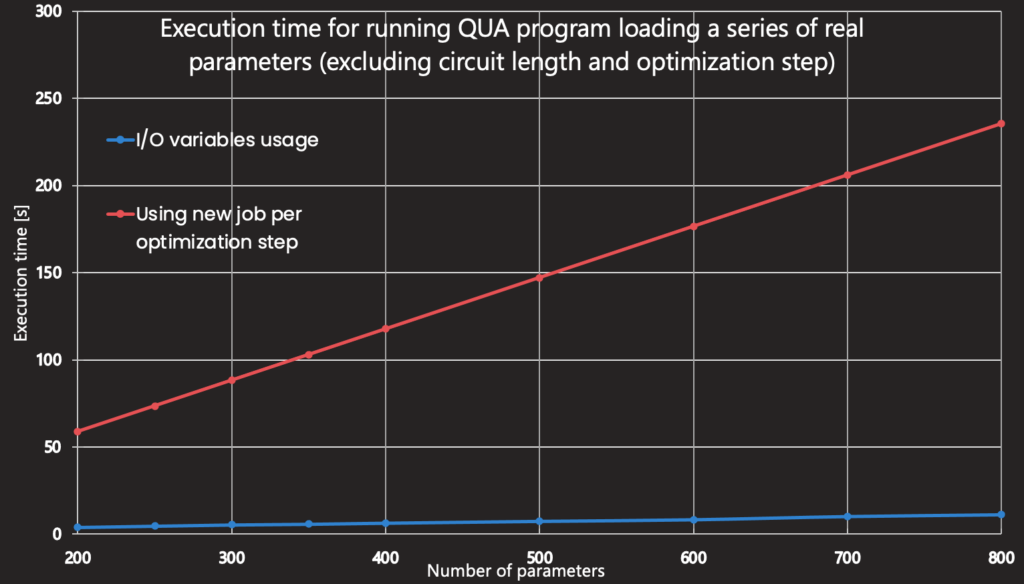
Benchmark of program execution comparing traditional setting for VQAs (one job to be run for each parameter update step) and the usage of I/O variables, featured in QOP architecture
We can quickly see how playing with this feature and many others, such as precompilation, will play an essential role in the near future in running scalable hybrid classical-quantum circuits.
Conclusion
Many more details can again be found in my thesis, but the key point here is that using the QOP gives you many improvements in the overall runtime performance of those VQAs with no additional complexity.
There are grounds for pushing the research even further by involving optimal control techniques in the algorithm framework through the real-time capabilities of the QOP. But this is a story for another day!
I don’t know about you, but I can’t wait to see quantum advantage emerging with those algorithms, and I bet that pulse control has a lot of say in the matter!
References:
[1] A Quantum Approximate Optimization Algorithm, Farhi et al., 2014
[2] Efficient Z-Gates for Quantum Computing, McKay et al., 2017
[3] Variational Quantum Algorithms – How do they work?, Michał Stęchły, 2020