Understanding a Superconducting Qubit Readout with QUA

In collaboration with Gal Winer

Over two and a half days at the end of October ’21, a group of (mostly) physics graduate students gathered in the beautiful and historic city of Heidelberg, Germany, for a great event: The “Quantum Idea Factory,” run by the EFEQT program. Alongside mentors from prestigious research institutes in the European Quantum community (Heidelberg, Karlsruhe Institute of Technology, and Amsterdam University), the Quantum Machines team was thrilled to join this program and have the opportunity to influence brilliant young quantum minds. Below is the account of one of the promising physicists we had the pleasure to collaborate with, Pierre Guichard from Strasbourg University. First, let’s kick this off with some general background information!

What is the EFEQT program?

The EFEQT program is a one-year complimentary training program for select students studying for a Master’s degree at a European university. It supplies accredited training modules and a certificate backed by top European research and education institutions and is supported by the Quantum Flagship’s Quantum Technology Education Coordination and Support Action (QTEdu CSA). EFEQT students can follow blended courses in quantum science and technology, allowing them to broaden their vision of physics outside of their university’s scope. 

What is the Quantum Idea Factory?

The “Quantum Idea Factory” is an event run by the EFEQT program. It is a learning experience at the intersection of rigorous academic research and free interdisciplinary exploration. Select students and young researchers have the chance to take part in a scientific hackathon, which enables the development of practical skills and a visionary mindset in crucial areas of quantum science and technologies.

What was your team’s project during the Quantum Idea Factory? 

Our team consisted of a group of five students from different backgrounds and universities: Jacopo De Santis (Technical University of Munich), Marcel Kern (University of Heidelberg), Maximilian Kramer (Freie Universtät Berlin), Andres Vega (Universitat de Barcelona), and myself, Pierre Guichard (University of Strasbourg). 

The Quantum Idea Factory especially caught my interest as a way to meet people I wouldn’t typically work with at Strasbourg and also as an opportunity to gather information from both industry and academic professionals.

During our stay in Heidelberg, our small group worked together to transform raw research ideas into well-rounded concepts for research projects or innovative solutions to address fundamental quantum science and technology challenges. 

Part 1: Characterizing a high-fidelity single-qubit rotation on a superconducting qubit

The main challenge we faced was the characterization of a high-fidelity single-qubit rotation on a superconducting qubit. Since superconducting qubits are all unique, we need a way to characterize them.

But first, what is a superconducting qubit, and how does the readout mechanism work?

Everyone knows the Hamiltonian of the Quantum Harmonic Oscillator (QHO): \(H= \hbar \omega_r \left( a^\dagger a+\frac{1}{2} \right)\), where \(a^\dagger\) is the creation operator, \(a\) is the annihilation operator, and \(\omega_r\) is the resonant frequency of the system. The linear characteristics of the QHO place a natural limitation on its applications for processing quantum information. Before we can use the system as a qubit, we need to define a computational subspace consisting of only two energy states (usually the two lowest energy eigenstates) in between which transitions can be driven without exciting other levels in the system. Since many gate operations, such as single-qubit gates, depend on frequency selectivity, the equidistant level-spacing of the QHO poses a practical limitation. To mitigate the problem of unwanted dynamics involving non-computational states, we need to add anharmonicity (or nonlinearity) into our system.

In short, to be individually addressable, we need the transition frequencies \(\omega_q^{0\to 1}\) and \(\omega_q^{1\to 2}\) to be sufficiently different. To introduce the nonlinearity required to modify the harmonic potential, we use the Josephson junction – a nonlinear, dissipation-less circuit element that forms the backbone in superconducting circuits. Then, we get a modified Hamiltonian, \(H= 4E_cn^2 –E_J \cos(\phi)\), where \(E_C\) is the total capacitance, and \(E_J\) is the Josephson energy. After introducing the Josephson junction in the circuit, the potential energy no longer takes a manifested parabolic form (from which the harmonic spectrum originates) but rather features a cosinusoidal form:

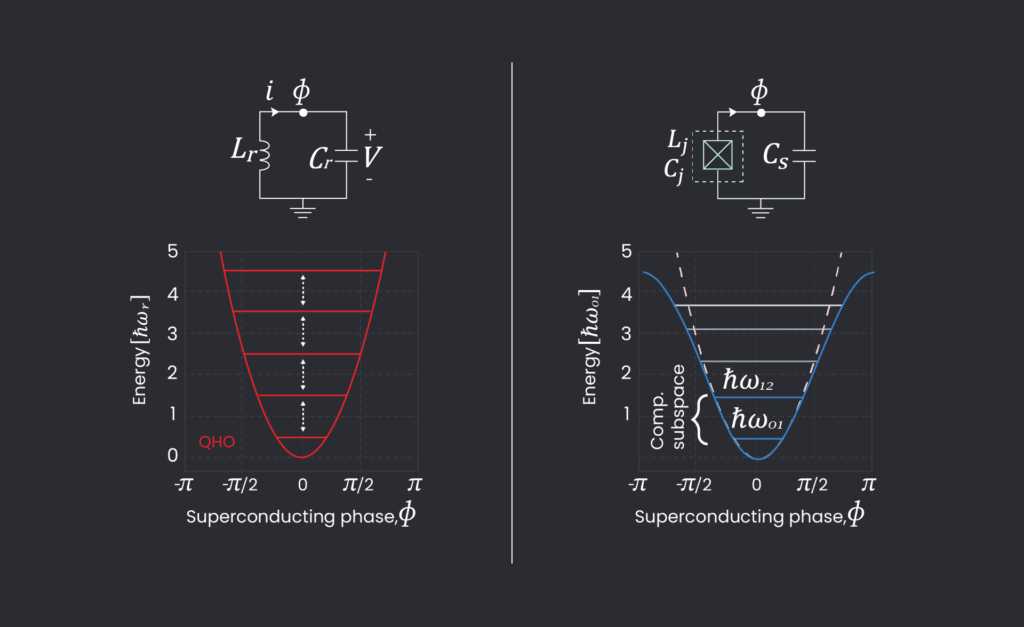
A common strategy to read out a qubit consists of coupling it dispersively to a resonator so that the qubit states\(\left|{0}\right\rangle\) and\(\left|{1}\right\rangle\) shift the resonance frequency differently. We can detect the frequency change by measuring the phase of a microwave pulse reflected on or transmitted through the resonator. 

Part 2: QUA and the quantum simulator

We used QUA, Quantum Machine’s pulse-level quantum coding language, to make a simulation. As someone accustomed to programming with Python and C++, I was pleasantly surprised by my experience learning to code with QUA. Since QUA is embedded within Python, it’s straightforward to learn and only took the group about half a day to be comfortable programming with it. The software stack provided with QUA includes a compiler and simulator, which can take a QUA program and simulate the pulse output, even without any hardware. In addition, it consists of a quantum simulator, which can take the generated pulses and simulate the state of a quantum system that receives those pulses, so you can do exciting work even if you don’t have a qubit at hand. The use of QUA and the quantum simulator helped us to simulate a qubit readout, and we received simple yet good results that I’ve included below.

We started with Rabi’s oscillation (the cyclic behavior of a two-level quantum system in the presence of an oscillatory driving field). It is always a great exercise to make it appear, and that’s just what we did:

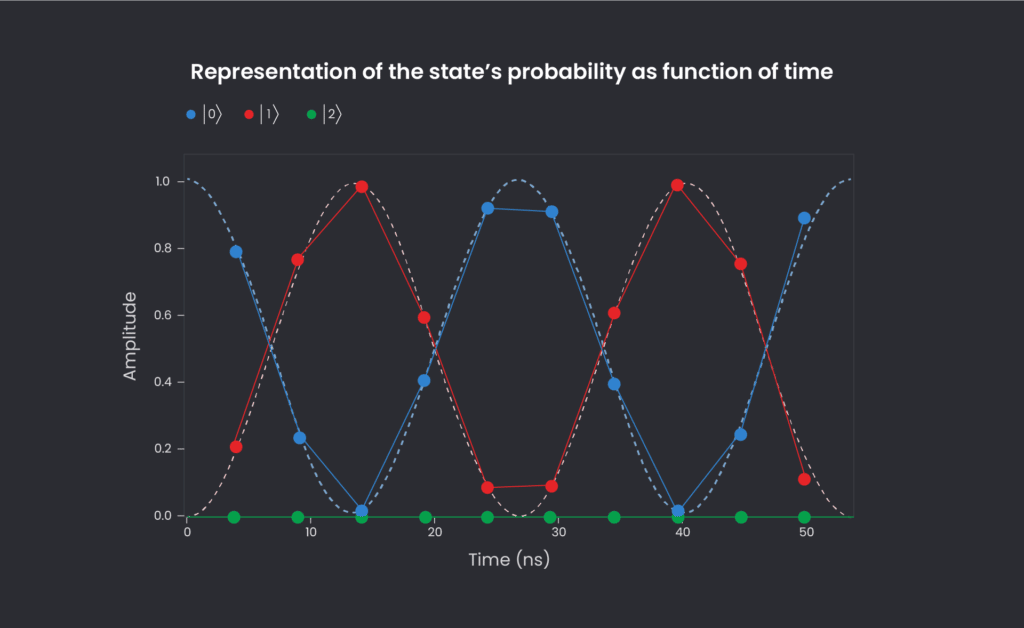
We indeed recover the theoretical fit (something proportional to a sinus squared) plotted out in a dashed line.

Throughout the project, we learned how to make qubit characterization with an IQ Blob single-qubit readout, and we also succeeded in making some simulations to see those, as can be seen in this plot:

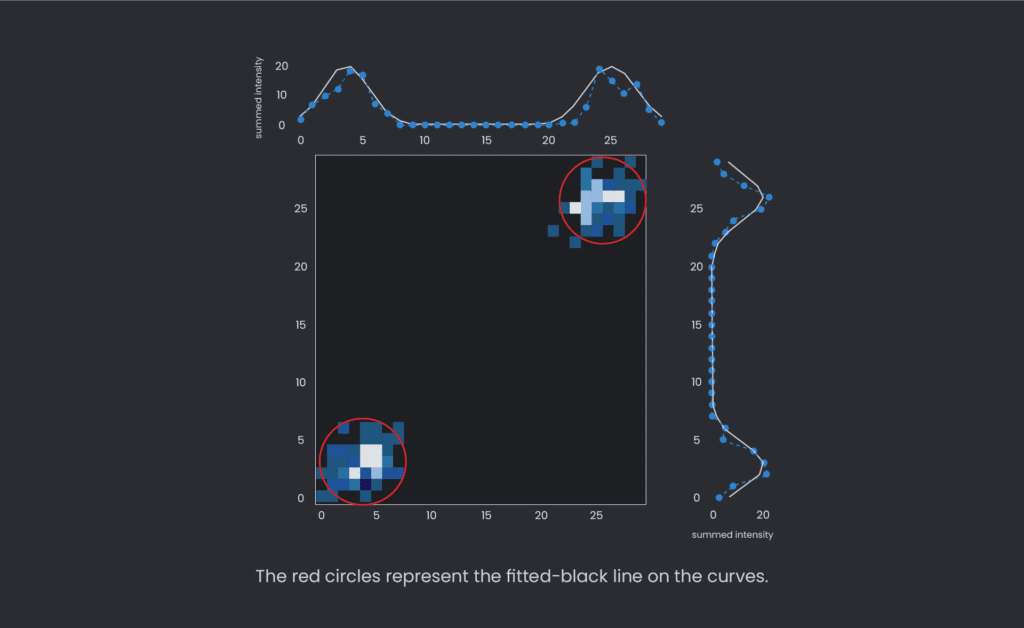
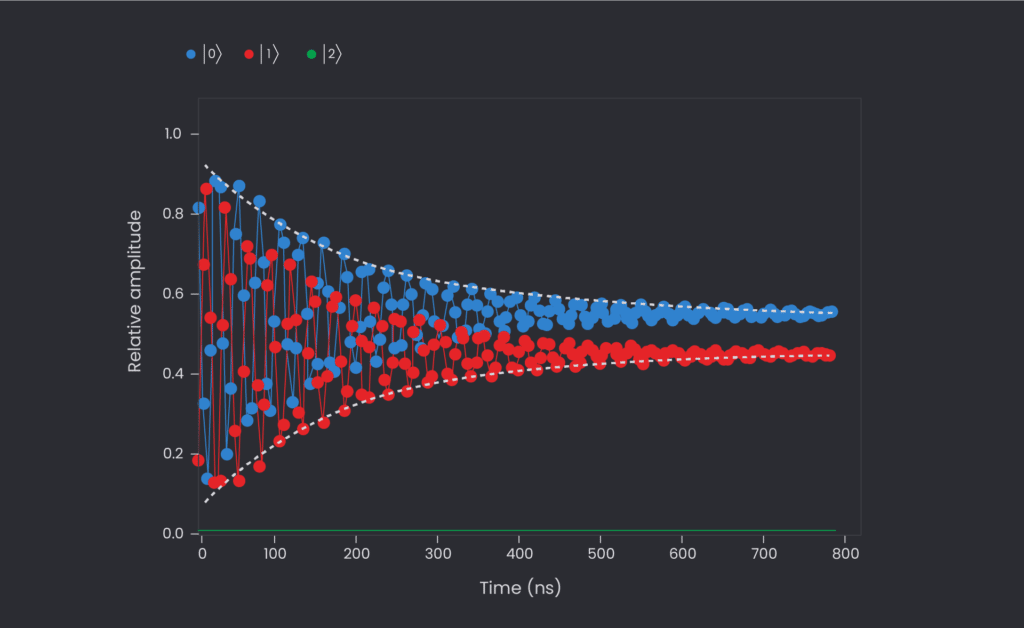
Additionally, when we add some noise within the system (making it more real as all systems have some noise), we should have a decoherence process going on, and although a bit of shift-up for the state \(\left|{0}\right\rangle\) and shift-down for\(\left|{1}\right\rangle\). By including such noise processes using the quantum simulator, we recovered the convergence of the two pure states in a 50% mixture state.

Part 3: Conclusion

All in all, our group project was a success! Not only did we learn about quantum science and technology from both academic and industrial perspectives, but we also had the chance to test it all out with our own hands, from learning the basics of qubit readout to discovering how to program with QUA. With direct guidance from Gal, the Quantum Machines Libraries Team Lead, I broadened my practical skills and strengthened my innovative mindset. The Quantum Idea Factory was a fulfilling event to participate in, and I would recommend it to anyone who’d like to get hands-on experience in turning research ideas into reality.